
已知定義域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/6a/4/11v3z2.png" style="vertical-align:middle;" />的函數(shù) 同時(shí)滿足以下三個(gè)條件:
同時(shí)滿足以下三個(gè)條件:
①對(duì)任意的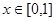 ,總有
,總有 ;
;
②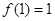 ;
;
③當(dāng)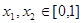 ,且
,且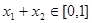 時(shí),
時(shí),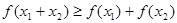 成立.
成立.
稱這樣的函數(shù)為“友誼函數(shù)”.
請(qǐng)解答下列各題:
(1)已知 為“友誼函數(shù)”,求
為“友誼函數(shù)”,求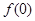 的值;
的值;
(2)函數(shù)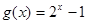 在區(qū)間
在區(qū)間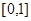 上是否為“友誼函數(shù)”?請(qǐng)給出理由;
上是否為“友誼函數(shù)”?請(qǐng)給出理由;
(3)已知 為“友誼函數(shù)”,假定存在
為“友誼函數(shù)”,假定存在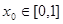 ,使得
,使得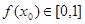 ,且
,且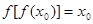 ,求證:
,求證: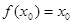 .
.
(1)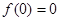 ;(2)
;(2) 在
在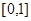 上為友誼函數(shù);(3)證明過(guò)程見(jiàn)解析.
上為友誼函數(shù);(3)證明過(guò)程見(jiàn)解析.
解析試題分析:(1)賦值可考慮取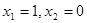 ,代入
,代入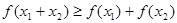 ,可得
,可得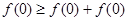 ,由已知
,由已知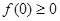 ,可得
,可得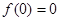 .
.
(2)要判斷函數(shù)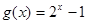 在區(qū)間
在區(qū)間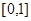 上是否為“友誼函數(shù),只要檢驗(yàn)函數(shù)
上是否為“友誼函數(shù),只要檢驗(yàn)函數(shù)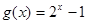 在
在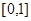 上是否滿足(1)
上是否滿足(1) ;(2)
;(2)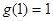 ;(3)
;(3)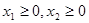 ,且
,且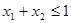 時(shí),有
時(shí),有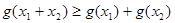 即可.
即可.
(3)由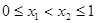 ,則
,則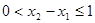 ,故有
,故有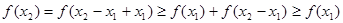 ,即得結(jié)論成立;
,即得結(jié)論成立;
(1)令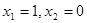 ,則
,則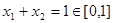 .由③,得
.由③,得 ,即
,即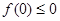 .又由①,得
.又由①,得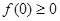 ,所以
,所以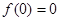 .
.
(2) 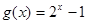 是友誼函數(shù).任取
是友誼函數(shù).任取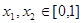 ,
,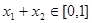 ,有
,有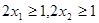 .則
.則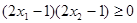 .即
.即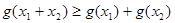 .又
.又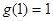 ,故
,故 在
在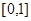 上為友誼函數(shù).
上為友誼函數(shù).
(3)取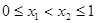 ,則
,則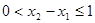 .因此,
.因此,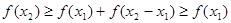 .假設(shè)
.假設(shè)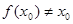 ,若
,若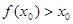 ,則
,則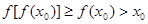 .若
.若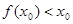 ,則
,則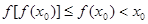 .都與題設(shè)矛盾,因此
.都與題設(shè)矛盾,因此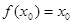 .
.
考點(diǎn):函數(shù)恒成立問(wèn)題.


 輕巧奪冠周測(cè)月考直通名校系列答案
輕巧奪冠周測(cè)月考直通名校系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)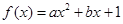 (
( 為實(shí)數(shù),
為實(shí)數(shù),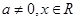 ),
),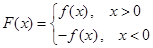 ,⑴若
,⑴若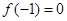 ,且函數(shù)
,且函數(shù) 的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/d0/e/1ap354.png" style="vertical-align:middle;" />,求
的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/d0/e/1ap354.png" style="vertical-align:middle;" />,求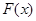 的表達(dá)式;
的表達(dá)式;
⑵設(shè) ,且函數(shù)
,且函數(shù) 為偶函數(shù),求證:
為偶函數(shù),求證: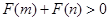 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
甲、乙兩個(gè)工廠,甲廠位于一直線河岸的岸邊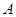 處,乙廠與甲廠在河的同側(cè),乙廠位于離河岸40千米的
處,乙廠與甲廠在河的同側(cè),乙廠位于離河岸40千米的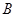 處,乙廠到河岸的垂足
處,乙廠到河岸的垂足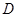 與
與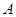 相距50千米,兩廠要在此岸邊
相距50千米,兩廠要在此岸邊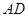 之間合建一個(gè)供水站
之間合建一個(gè)供水站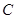 ,從供水站到甲廠和乙廠的水管費(fèi)用分別為每千米3
,從供水站到甲廠和乙廠的水管費(fèi)用分別為每千米3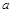 元和5
元和5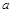 元,若
元,若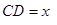 千米,設(shè)總的水管費(fèi)用為
千米,設(shè)總的水管費(fèi)用為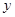 元,如圖所示,
元,如圖所示,
(1)寫(xiě)出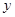 關(guān)于
關(guān)于 的函數(shù)表達(dá)式;
的函數(shù)表達(dá)式;
(2)問(wèn)供水站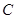 建在岸邊何處才能使水管費(fèi)用最省?
建在岸邊何處才能使水管費(fèi)用最省? 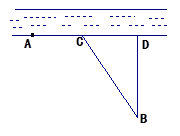
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
某漁業(yè)公司年初用49萬(wàn)元購(gòu)買一艘捕魚(yú)船,第一年各種費(fèi)用6萬(wàn)元,以后每年都增加2萬(wàn)元,每年捕魚(yú)收益25萬(wàn)元.
(1)問(wèn)第幾年開(kāi)始獲利?
(2)若干年后,有兩種處理方案:①年平均獲利最大時(shí),以18萬(wàn)元出售該漁船;②總純收入獲利最大時(shí),以9萬(wàn)元出售該漁船.問(wèn)哪種方案最合算?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知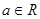 ,函數(shù)
,函數(shù)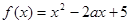 .
.
⑴若不等式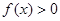 對(duì)任意
對(duì)任意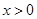 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)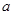 的最值范圍;
的最值范圍;
⑵若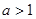 ,且函數(shù)
,且函數(shù) 的定義域和值域均為
的定義域和值域均為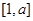 ,求實(shí)數(shù)
,求實(shí)數(shù)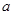 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
設(shè)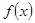 是定義在
是定義在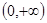 上的函數(shù),且
上的函數(shù),且 ,對(duì)任意
,對(duì)任意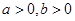 ,若經(jīng)過(guò)點(diǎn)
,若經(jīng)過(guò)點(diǎn)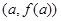 ,
,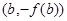 的直線與
的直線與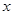 軸的交點(diǎn)為
軸的交點(diǎn)為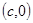 ,則稱
,則稱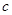 為
為 關(guān)于函數(shù)
關(guān)于函數(shù)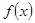 的平均數(shù),記為
的平均數(shù),記為 ,例如,當(dāng)
,例如,當(dāng)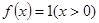 時(shí),可得
時(shí),可得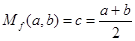 ,即
,即 為
為 的算術(shù)平均數(shù).
的算術(shù)平均數(shù).
當(dāng) 時(shí),
時(shí), 為
為 的幾何平均數(shù);
的幾何平均數(shù);
當(dāng) 時(shí),
時(shí), 為
為 的調(diào)和平均數(shù)
的調(diào)和平均數(shù) ;
;
(以上兩空各只需寫(xiě)出一個(gè)符合要求的函數(shù)即可)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
設(shè) (
(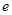 是自然對(duì)數(shù)的底數(shù),
是自然對(duì)數(shù)的底數(shù),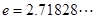 ),且
),且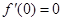 .
.
(1)求實(shí)數(shù)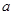 的值,并求函數(shù)
的值,并求函數(shù)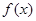 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)設(shè)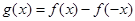 ,對(duì)任意
,對(duì)任意 ,恒有
,恒有 成立.求實(shí)數(shù)
成立.求實(shí)數(shù) 的取值范圍;
的取值范圍;
(3)若正實(shí)數(shù)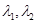 滿足
滿足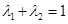 ,
,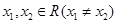 ,試證明:
,試證明: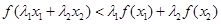 ;并進(jìn)一步判斷:當(dāng)正實(shí)數(shù)
;并進(jìn)一步判斷:當(dāng)正實(shí)數(shù) 滿足
滿足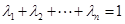
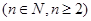 ,且
,且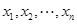 是互不相等的實(shí)數(shù)時(shí),不等式
是互不相等的實(shí)數(shù)時(shí),不等式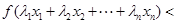
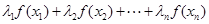 是否仍然成立.
是否仍然成立.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
某造紙廠擬建一座底面圖形為矩形且面積為162平方米的三級(jí)污水處理池,池的深度一定(平面圖如圖所示),如果池四周圍墻建造單價(jià)為400元/米,中間兩道隔墻建造單價(jià)為248元/米,池底建造單價(jià)為80元/平方米,水池所有墻的厚度忽略不計(jì).
(1)試設(shè)計(jì)污水處理池的長(zhǎng)和寬,使總造價(jià)最低,并求出最低總造價(jià);
(2)若由于地形限制,該池的長(zhǎng)和寬都不能超過(guò)16米,試設(shè)計(jì)污水處理池的長(zhǎng)和寬,使總造價(jià)最低,并求出最低總造價(jià).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com