
【題目】在平面直角坐標系xOy中,已知向量 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),
), ![]() =(sinx,cosx),x∈(0,
=(sinx,cosx),x∈(0, ![]() ).
).
(1)若 ![]() ⊥
⊥ ![]() ,求tanx的值;
,求tanx的值;
(2)若 ![]() 與
與 ![]() 的夾角為
的夾角為 ![]() ,求x的值.
,求x的值.
【答案】
(1)解:若 ![]() ⊥
⊥ ![]() ,
,
則 ![]()
![]() =(
=( ![]() ,﹣
,﹣ ![]() )(sinx,cosx)=
)(sinx,cosx)= ![]() sinx﹣
sinx﹣ ![]() cosx=0,
cosx=0,
即 ![]() sinx=
sinx= ![]() cosx
cosx
sinx=cosx,即tanx=1;
(2)解:∵| ![]() |=
|= ![]() ,|
,| ![]() |=
|= ![]() =1,
=1, ![]()
![]() =(
=( ![]() ,﹣
,﹣ ![]() )(sinx,cosx)=
)(sinx,cosx)= ![]() sinx﹣
sinx﹣ ![]() cosx,
cosx,
∴若 ![]() 與
與 ![]() 的夾角為
的夾角為 ![]() ,
,
則 ![]()
![]() =|
=| ![]() ||
|| ![]() |cos
|cos ![]() =
= ![]() ,
,
即 ![]() sinx﹣
sinx﹣ ![]() cosx=
cosx= ![]() ,
,
則sin(x﹣ ![]() )=
)= ![]() ,
,
∵x∈(0, ![]() ).
).
∴x﹣ ![]() ∈(﹣
∈(﹣ ![]() ,
, ![]() ).
).
則x﹣ ![]() =
= ![]()
即x= ![]() +
+ ![]() =
= ![]()
【解析】(1)若 ![]() ⊥
⊥ ![]() ,則
,則 ![]()
![]() =0,結合三角函數的關系式即可求tanx的值;(2)若
=0,結合三角函數的關系式即可求tanx的值;(2)若 ![]() 與
與 ![]() 的夾角為
的夾角為 ![]() ,利用向量的數量積的坐標公式進行求解即可求x的值.
,利用向量的數量積的坐標公式進行求解即可求x的值.
【考點精析】根據題目的已知條件,利用數量積表示兩個向量的夾角的相關知識可以得到問題的答案,需要掌握設![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 與
與![]() 的夾角,則
的夾角,則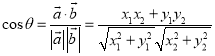 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,邊長為2的正方形ABCD中, 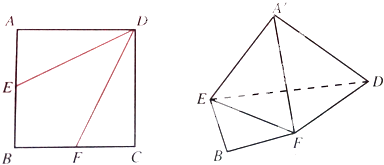
(1)點E是AB的中點,點F是BC的中點,將△AED,△DCF分別沿DE,DF折起,使A,C兩點重合于點A′.求證:A′D⊥EF
(2)當BE=BF= ![]() BC時,求三棱錐A′﹣EFD的體積.
BC時,求三棱錐A′﹣EFD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,以原點為圓心,橢圓的短半軸為半徑的圓與直線x﹣y+
,以原點為圓心,橢圓的短半軸為半徑的圓與直線x﹣y+ ![]() =0相切,過點P(4,0)且不垂直于x軸直線l與橢圓C相交于A、B兩點.
=0相切,過點P(4,0)且不垂直于x軸直線l與橢圓C相交于A、B兩點.
(1)求橢圓C的方程;
(2)求 ![]() 的取值范圍;
的取值范圍;
(3)若B點關于x軸的對稱點是E,證明:直線AE與x軸相交于定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(ωx+φ)+b的圖象如圖,則f(x)的解析式和S=f(1)+f(2)+f(3)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分別為( ) 
A.f(x)= ![]() sin
sin ![]() x+1,S=2016
x+1,S=2016
B.f(x)= ![]() cos
cos ![]() x+1,S=2016
x+1,S=2016
C.f(x)= ![]() sin
sin ![]() x+1,S=2016.5
x+1,S=2016.5
D.f(x)= ![]() cos
cos ![]() x+1,S=2016.5
x+1,S=2016.5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖的多面體中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中點. 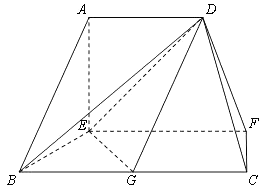
(1)求證:AB∥平面DEG;
(2)求證:BD⊥EG;
(3)求二面角C﹣DF﹣E的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a為正的常數,函數f(x)=|ax﹣x2|+lnx.
(1)若a=2,求函數f(x)的單調遞增區間;
(2)設g(x)= ![]() ,求g(x)在區間[1,e]上的最小值.(e≈2.71828為自然對數的底數)
,求g(x)在區間[1,e]上的最小值.(e≈2.71828為自然對數的底數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數),以
為參數),以![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,且直線
,且直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(Ⅰ)求曲線![]() 的直角坐標方程及直線
的直角坐標方程及直線![]() 恒過的定點
恒過的定點![]() 的坐標;
的坐標;
(Ⅱ)在(Ⅰ)的條件下,若![]() ,求直線
,求直線![]() 的普通方程.
的普通方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com