
【題目】設(shè)函數(shù)![]() .
.
(1)若不等式![]() 的解集為
的解集為![]() ,求實數(shù)
,求實數(shù)![]() 、
、![]() 的值;
的值;
(2)解不等式![]() .
.
【答案】(1) 
(2) ![]() 時解集為
時解集為![]() ,
,![]() 時解集為
時解集為![]() ,
,![]() 時解集為
時解集為![]() ,
,![]() 時解集為
時解集為![]() ,
,![]() 時解集為
時解集為![]()
【解析】
試題分析:(1)根據(jù)一元二次不等式的解集,利用根與系數(shù)的關(guān)系,即可求出實數(shù)a、m的值;
(2)不等式化為(ax-1)(x-1)<0,討論a=0和a>0、a<0時,求出不等式f(x)<0的解集即可
試題解析:⑴∵![]() ,
,
∴不等式![]() 等價于
等價于![]() ,
,
依題意知不等式![]() 的解集為
的解集為![]() ,
,
∴![]() 且1和2為方程
且1和2為方程![]() 的兩根,
的兩根,
∴ ,
,
解得 ,
,
∴實數(shù)![]() 、
、![]() 的值分別為
的值分別為![]() 、
、![]() ,
,
⑵不等式![]() 可化為
可化為![]() ,
,
(ⅰ)當(dāng)![]() 時,不等式
時,不等式![]() 等價于
等價于![]() ,解得
,解得![]() ,故原不等式的解集為
,故原不等式的解集為![]() , 7分
, 7分
(ⅱ)當(dāng)![]() 時,不等式
時,不等式![]() 等價于
等價于![]() ,
,
①當(dāng)![]() 時
時![]() ,不等式
,不等式![]() 的解集為
的解集為![]() ,即原不等式的解集為
,即原不等式的解集為![]() ,
,
②當(dāng)![]() 時,不等式
時,不等式![]() 的解集為
的解集為![]() ,即原不等式的解集為
,即原不等式的解集為![]() ,
,
③當(dāng)![]() 時
時![]() ,不等式
,不等式![]() 的解集為
的解集為![]() ,即原不等式的解集為
,即原不等式的解集為![]() ,
,
(ⅲ)當(dāng)![]() 時,不等式
時,不等式![]() 等價于
等價于![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴不等式![]() 的解集為
的解集為![]() ,即原不等式的解集為
,即原不等式的解集為![]() ,
,
綜上所述,當(dāng)![]() 時不等式
時不等式![]() 的的解集為
的的解集為![]() ,
,
當(dāng)![]() 時不等式
時不等式![]() 的的解集為
的的解集為![]() ,
,
當(dāng)![]() 時不等式
時不等式![]() 的的解集為
的的解集為![]() ,
,
當(dāng)![]() 時不等式
時不等式![]() 的的解集為
的的解集為![]() ,
,
當(dāng)![]() 時不等式
時不等式![]() 的的解集為
的的解集為![]() 。
。


 海淀課時新作業(yè)金榜卷系列答案
海淀課時新作業(yè)金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標(biāo)準(zhǔn)練系列答案
輕松課堂標(biāo)準(zhǔn)練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分13分)
如圖,⊙O在平面![]() 內(nèi),AB是⊙O的直徑,
內(nèi),AB是⊙O的直徑,![]() 平面
平面![]() ,C為圓周上不同于A、B的任意一點,M,N,Q分別是PA,PC,PB的中點.
,C為圓周上不同于A、B的任意一點,M,N,Q分別是PA,PC,PB的中點.

(1)求證:![]() 平面
平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)求證:![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}的首項a1=2,且an=2an﹣1﹣1(n∈N* , N≥2)
(1)求證:數(shù)列{an﹣1}為等比數(shù)列;并求數(shù)列{an}的通項公式;
(2)求數(shù)列{nan﹣n}的前n項和Sn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=x3﹣3ax2﹣9a2x+a3 . 若a> ![]() ,且當(dāng)x∈[1,4a]時,|f′(x)|≤12a恒成立,則a的取值范圍為( )
,且當(dāng)x∈[1,4a]時,|f′(x)|≤12a恒成立,則a的取值范圍為( )
A.( ![]() ,
, ![]() ]
]
B.( ![]() ,1]
,1]
C.[﹣ ![]() ,1]
,1]
D.[0, ![]() ]
]
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校高三數(shù)學(xué)競賽初賽考試后,對考生的成績進行統(tǒng)計(考生成績均不低于90分,滿分150分),將成績按如下方式分成六組,第一組[90,100)、第二組[100,110)…第六組[140,150].圖(1)為其頻率分布直方圖的一部分,若第四、五、六組的人數(shù)依次成等差數(shù)列,且第六組有4人. (Ⅰ)請補充完整頻率分布直方圖,并估計這組數(shù)據(jù)的平均數(shù)M;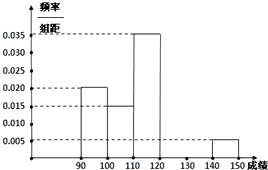
(Ⅱ)若不低于120分的同學(xué)進入決賽,不低于140分的同學(xué)為種子選手,完成下面2×2
列聯(lián)表(即填寫空格處的數(shù)據(jù)),并判斷是否有99%的把握認(rèn)為“進入決賽的同學(xué)
成為種子選手與專家培訓(xùn)有關(guān)”.
| [140,150] | 合計 | |
參加培訓(xùn) | 5 | 8 | |
未參加培訓(xùn) | |||
合計 | 4 |
附: ![]()
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知曲線C的參數(shù)方程為 ![]() (θ為參數(shù)).以原點O為極點,x軸的非負(fù)半軸為極軸建立極坐標(biāo)方程.
(θ為參數(shù)).以原點O為極點,x軸的非負(fù)半軸為極軸建立極坐標(biāo)方程.
(1)求曲線C的極坐標(biāo)方程;
(2)若直線l:θ=α(α∈[0,π),ρ∈R)與曲線C相交于A,B兩點,設(shè)線段AB的中點為M,求|OM|的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=2lnx﹣ax+a(a∈R).
(1)討論f(x)的單調(diào)性;
(2)若f(x)≤0恒成立,證明:當(dāng)0<x1<x2時, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(1)已知圓![]() 的圓心是直線
的圓心是直線![]() 與
與![]() 軸的交點,且與直線
軸的交點,且與直線![]() 相切,求圓
相切,求圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)已知圓![]() ,直線
,直線![]() 過點
過點![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,若
兩點,若![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com