
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD的平行四邊形,∠ADC=60°, ![]() ,PA⊥面ABCD,E為PD的中點.
,PA⊥面ABCD,E為PD的中點.
(Ⅰ)求證:AB⊥PC
(Ⅱ)若PA=AB= ![]() ,求三棱錐P﹣AEC的體積.
,求三棱錐P﹣AEC的體積.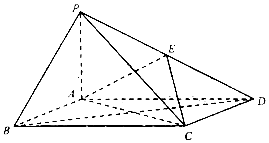
【答案】(Ⅰ)證明:因為PA⊥面ABCD,又AB平面ABCD,
所以AB⊥PA,
又因為∠ABC=∠ADC=60°, ![]() ,
,
在△ABC中,由余弦定理有:
AC2=AB2+BC2﹣2ABBCcos60°=BC2﹣AB2
所以AB2+AC2=BC2,
即:AB⊥AC,
又因為PA∩AC=A,又PA平面PAC,AC平面PAC,
所以AB⊥平面PAC,
又PC平面PAC,所以AB⊥PC.
(Ⅱ)解:由已知有: ![]() ,
,
所以PA=AB=2,AD=4,因為PA⊥面ABCD
且E為PD的中點,所以E點到平面ADC的距離為 ![]() ,
,
所以三棱錐P﹣AEC的體積:
VP﹣AEC=VD﹣AEC=VE﹣ADC= ![]()
= ![]() ×
× ![]() .
.
【解析】(1)因為PA⊥面ABCD,則AB⊥PA,根據邊角的大小關系,由余弦定理可證出△ABC為直角三角形,即AB⊥AC,從而可證出AB⊥面PAC,即AB⊥PC,(2)由已知可得出其各邊的大小,由于E為PD的中點,則不難得出E到面ADC的距離為1,VP﹣AEC=VD﹣AEC=VE﹣ADC= ![]() S △ A D C,即可得出結果.
S △ A D C,即可得出結果.
【考點精析】本題主要考查了空間中直線與直線之間的位置關系的相關知識點,需要掌握相交直線:同一平面內,有且只有一個公共點;平行直線:同一平面內,沒有公共點;異面直線: 不同在任何一個平面內,沒有公共點才能正確解答此題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】設△ABC的內角A,B,C所對的邊分別為a,b,c且acosB=4,bsinA=3.
(1)求tanB及邊長a的值;
(2)若△ABC的面積S=9,求△ABC的周長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,MCN是某海灣旅游區的一角,為營造更加優美的旅游環境,旅游區管委會決定建立面積為4 ![]() 平方千米的三角形主題游戲樂園ABC,并在區域CDE建立水上餐廳.已知∠ACB=120°,∠DCE=30°.
平方千米的三角形主題游戲樂園ABC,并在區域CDE建立水上餐廳.已知∠ACB=120°,∠DCE=30°.
(1)設AC=x,AB=y,用x表示y,并求y的最小值;
(2)設∠ACD=θ(θ為銳角),當AB最小時,用θ表示區域CDE的面積S,并求S的最小值.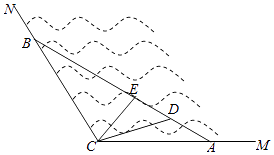
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b,c分別是△ABC的角A,B,C所對的邊,且c=2,C= ![]() .
.
(1)若△ABC的面積等于 ![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B﹣A)=2sin2A,求A的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:(x+2)2+y2=5,直線l:mx﹣y+1+2m=0,m∈R.
(1)求證:對m∈R,直線l與圓C總有兩個不同的交點A、B;
(2)求弦AB的中點M的軌跡方程,并說明其軌跡是什么曲線;
(3)是否存在實數m,使得圓C上有四點到直線l的距離為 ![]() ?若存在,求出m的范圍;若不存在,說明理由.
?若存在,求出m的范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() +ax,x>1.
+ax,x>1.
(1)若函數f(x)在 ![]() 處取得極值,求a的值;
處取得極值,求a的值;
(2)若方程(2x﹣m)lnx+x=0在(1,e]上有兩個不等實根,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)是定義在[﹣1,1]上的奇函數,f(﹣1)=﹣1,且對任意a,b∈[﹣1,1],當a≠b時,都有 ![]() ;
;
(1)解不等式f ![]() ;
;
(2)若f(x)≤m2﹣2km+1對所有x∈[﹣1,1],k∈[﹣1,1]恒成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com