
【題目】已知函數![]() 的零點構成一個公差為
的零點構成一個公差為![]() 的等差數列,把函數
的等差數列,把函數![]() 的圖象沿
的圖象沿![]() 軸向右平移
軸向右平移![]() 個單位,得到函數
個單位,得到函數![]() 的圖象.關于函數
的圖象.關于函數![]() ,下列說法正確的是( )
,下列說法正確的是( )
A. 在![]() 上是增函數B. 其圖象關于直線
上是增函數B. 其圖象關于直線![]() 對稱
對稱
C. 函數![]() 是偶函數D. 在區間
是偶函數D. 在區間![]() 上的值域為
上的值域為![]()
【答案】D
【解析】
化簡f(x)=2sin(ωx![]() ),由三角函數圖象的平移得:g(x)=2sin2x,
),由三角函數圖象的平移得:g(x)=2sin2x,
由三角函數圖象的性質得y=g(x)的單調性,對稱性,再由x![]() 時,求得函數g(x)值域得解.
時,求得函數g(x)值域得解.
f(x)=sinωx![]() cosωx=2sin(ωx
cosωx=2sin(ωx![]() ),
),
由函數f(x)的零點構成一個公差為![]() 的等差數列,
的等差數列,
則周期T=π,即ω=2,
即f(x)=2sin(2x![]() ),
),
把函數f(x)的圖象沿x軸向右平移![]() 個單位,得到函數g(x)的圖象,
個單位,得到函數g(x)的圖象,
則g(x)=2sin[2(x![]() )
)![]() ]=2sin2x,
]=2sin2x,
當![]() ≤2x≤
≤2x≤![]() ,即
,即![]() ≤x≤
≤x≤![]() , y=g(x)是減函數,故y=g(x)在[
, y=g(x)是減函數,故y=g(x)在[![]() ,
,![]() ]為減函數,
]為減函數,
當2x=![]() 即x
即x![]() (k∈Z),y=g(x)其圖象關于直線x
(k∈Z),y=g(x)其圖象關于直線x![]() (k∈Z)對稱,且為奇函數,
(k∈Z)對稱,且為奇函數,
故選項A,B,C錯誤,
當x![]() 時,2x∈[
時,2x∈[![]() ,
,![]() ],函數g(x)的值域為[
],函數g(x)的值域為[![]() ,2],
,2],
故選項D正確,
故選:D.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直角三角形ABC的三個頂點都在橢圓![]() 上,其中A(0,1)為直角頂點.若該三角形的面積的最大值為
上,其中A(0,1)為直角頂點.若該三角形的面積的最大值為![]() ,則實數a的值為_____.
,則實數a的值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓柱OO1底面半徑為1,高為π,ABCD是圓柱的一個軸截面.動點M從點B出發沿著圓柱的側面到達點D,其距離最短時在側面留下的曲線Γ如圖所示.將軸截面ABCD繞著軸OO1逆時針旋轉θ(0<θ<π)后,邊B1C1與曲線Γ相交于點P.
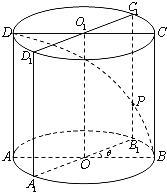
(1)求曲線Γ長度;
(2)當![]() 時,求點C1到平面APB的距離;
時,求點C1到平面APB的距離;
(3)是否存在θ,使得二面角D﹣AB﹣P的大小為![]() ?若存在,求出線段BP的長度;若不存在,請說明理由.
?若存在,求出線段BP的長度;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() ),曲線
),曲線![]() 的參數方程為
的參數方程為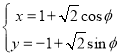 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)設曲線![]() 與曲線
與曲線![]() 的交點分別為
的交點分別為![]() ,求
,求![]() 的最大值及此時直線
的最大值及此時直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年春節期間,全國人民都在抗擊“新型冠狀病毒肺炎”的斗爭中.當時武漢多家醫院的醫用防護物資庫存不足,某醫院甚至面臨斷貨危機,南昌某生產商現有一批庫存的醫用防護物資,得知消息后,立即決定無償捐贈這批醫用防護物資,需要用A、B兩輛汽車把物資從南昌緊急運至武漢.已知從南昌到武漢有兩條合適路線選擇,且選擇兩條路線所用的時間互不影響.據調查統計2000輛汽車,通過這兩條路線從南昌到武漢所用時間的頻數分布表如下:
所用的時間(單位:小時) |
|
|
|
|
路線1的頻數 | 200 | 400 | 200 | 200 |
路線2的頻數 | 100 | 400 | 400 | 100 |
假設汽車A只能在約定交貨時間的前5小時出發,汽車B只能在約定交貨時間的前6小時出發(將頻率視為概率).為最大可能在約定時間送達這批物資,來確定這兩車的路線.
(1)汽車A和汽車B應如何選擇各自的路線.
(2)若路線1、路線2的“一次性費用”分別為3.2萬元、1.6萬元,且每車醫用物資生產成本為40萬元(其他費用忽略不計),以上費用均由生產商承擔,作為援助金額的一部分.根據這兩輛車到達時間分別計分,具體規則如下(已知兩輛車到達時間相互獨立,互不影響):
到達時間與約定時間的差x(單位:小時) |
|
|
|
該車得分 | 0 | 1 | 2 |
生產商準備根據運輸車得分情況給出現金排款,兩車得分和為0,捐款40萬元,兩車得分和每增加1分,捐款增加20萬元,若汽車A、B用(1)中所選的路線運輸物資,記該生產商在此次援助活動中援助總額為Y(萬元),求隨機變量Y的期望值,(援助總額![]() 一次性費用
一次性費用![]() 生產成本
生產成本![]() 現金捐款總額)
現金捐款總額)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩工人在同樣的條件下生產,日產量相等,每天出廢品的情況如下表:

則下列結論中正確的是 ( )
A. 甲生產的產品質量比乙生產的產品質量好一些
B. 乙生產的產品質量比甲生產的產品質量好一些
C. 兩人生產的產品質量一樣好
D. 無法判斷誰生產的產品質量好一些
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知,圖中直棱柱![]() 的底面是菱形,其中
的底面是菱形,其中![]() .又點
.又點![]() 分別在棱
分別在棱![]() 上運動,且滿足:
上運動,且滿足:![]() ,
,![]() .
.
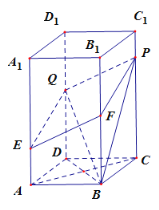
(1)求證:![]() 四點共面,并證明
四點共面,并證明![]() ∥平面
∥平面![]() .
.
(2)是否存在點![]() 使得二面角
使得二面角![]() 的余弦值為
的余弦值為![]() ?如果存在,求出
?如果存在,求出![]() 的長;如果不存在,請說明理由.
的長;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了了解學生對《3.12植樹節》活動節日的相關內容,學校進行了一次10道題的問卷調查,從該校學生中隨機抽取50人,統計了每人答對的題數,將統計結果分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五組,得到如下頻率分布直方圖.
五組,得到如下頻率分布直方圖.
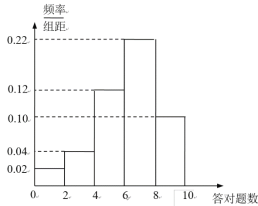
(1)若答對一題得10分,答錯和未答不得分,估計這50名學生成績的平均分;
(2)若從答對題數在![]() 內的學生中隨機抽取2人,求恰有1人答對題數在
內的學生中隨機抽取2人,求恰有1人答對題數在![]() 內的概率.
內的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com