
【題目】如圖,在多面體![]() 中,四邊形
中,四邊形![]() 是平行四邊形,平面
是平行四邊形,平面![]() 平面
平面![]() ,
,![]() 為正三角形,
為正三角形,![]() ,
,![]() ,
,![]() .
.
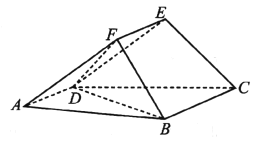
(1)證明:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)分別取![]() ,
,![]() 的中點連結
的中點連結![]() ,
,![]() ,
,![]() ,先證
,先證![]() ,再證
,再證![]() 平面
平面![]() ,然后可得
,然后可得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,可證平面
,可證平面![]() 平面
平面![]() ;
;
(2)先建立空間直角坐標系,然后分別求出平面![]() 的法向量為
的法向量為![]() 和平面
和平面![]() 的法向量為
的法向量為![]() ,然后代入公式
,然后代入公式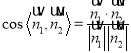 計算即可.
計算即可.
(1)如圖,分別取![]() ,
,![]() 的中點連結
的中點連結![]() ,
,![]() ,
,![]() ,
,
可得![]() ,
,![]() ,
,
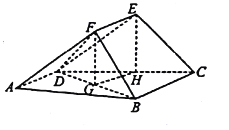
∵四邊形![]() 是平行四邊形,∴
是平行四邊形,∴![]() ,
,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴四邊形![]() 為平行四邊形,∴
為平行四邊形,∴![]() ,
,
又![]() 為正三角形,
為正三角形,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
滿足![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() ,又
,又![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)由(1)得建立如圖所示的空間直角坐標系![]() ,
,
由題意得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
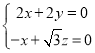 ,令
,令![]() ,則
,則![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,
,![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
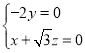 ,解得
,解得![]() ,令
,令![]() ,則
,則![]() ,
,
∴![]() ,
,
∴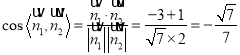 ,
,
∴平面![]() 與平面
與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() .
.


 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:高中數學 來源: 題型:
【題目】正態分布有極其廣泛的實際背景,生產與科學實驗中很多隨機變量的概率分布都可以近似地用正態分布來描述.例如,同一種生物體的身長、體重等指標.隨著“綠水青山就是金山銀山”的觀念不斷的深入人心,環保工作快速推進,很多地方的環境出現了可喜的變化.為了調查某水庫的環境保護情況,在水庫中隨機捕撈了100條魚稱重.經整理分析后發現,魚的重量x(單位:kg)近似服從正態分布![]() ,如圖所示,已知
,如圖所示,已知![]() .
.
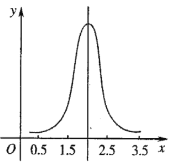
(Ⅰ)若從水庫中隨機捕撈一條魚,求魚的重量在![]() 內的概率;
內的概率;
(Ⅱ)(ⅰ)從捕撈的100條魚中隨機挑出6條魚測量體重,6條魚的重量情況如表.
重量范圍(單位:kg) |
|
|
|
條數 | 1 | 3 | 2 |
為了進一步了解魚的生理指標情況,從6條魚中隨機選出3條,記隨機選出的3條魚中體重在![]() 內的條數為X,求隨機變量X的分布列和數學期望;
內的條數為X,求隨機變量X的分布列和數學期望;
(ⅱ)若將選剩下的94條魚稱重做標記后立即放生.兩周后又隨機捕撈1000條魚,發現其中帶有標記的有2條.為了調整生態結構,促進種群的優化,預備捕撈體重在![]() 內的魚的總數的40%進行出售,試估算水庫中魚的條數以及應捕撈體重在
內的魚的總數的40%進行出售,試估算水庫中魚的條數以及應捕撈體重在![]() 內的魚的條數.
內的魚的條數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點![]() 為平面直角坐標系
為平面直角坐標系![]() 中的一個動點(其中
中的一個動點(其中![]() 為坐標系原點),點
為坐標系原點),點![]() 到定點
到定點![]() 的距離比到直線
的距離比到直線![]() 的距離大1,動點
的距離大1,動點![]() 的軌跡方程為
的軌跡方程為![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 、
、![]() 兩點.
兩點.
①若![]() ,求直線
,求直線![]() 的直線方程;
的直線方程;
②分別過點![]() ,
,![]() 作曲線
作曲線![]() 的切線且交于點
的切線且交于點![]() ,是否存在以
,是否存在以![]() 為圓心,以
為圓心,以![]() 為半徑的圓與經過點
為半徑的圓與經過點![]() 且垂直于直線
且垂直于直線![]() 的直線
的直線![]() 相交于
相交于![]() 、
、![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐![]() 中,PC⊥面ABCD,直角梯形ABCD中,∠B=∠C=90°,AB=4,CD=1,PC=2,點M在PB上且PB=4PM,PB與平面PCD所成角為60°.
中,PC⊥面ABCD,直角梯形ABCD中,∠B=∠C=90°,AB=4,CD=1,PC=2,點M在PB上且PB=4PM,PB與平面PCD所成角為60°.
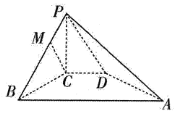
(1)求證:![]() 面
面![]() :
:
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() +
+![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為![]() ,直線l:x+2y=4與橢圓有且只有一個交點T.
,直線l:x+2y=4與橢圓有且只有一個交點T.
(I)求橢圓C的方程和點T的坐標;
(Ⅱ)O為坐標原點,與OT平行的直線l′與橢圓C交于不同的兩點A,B,直線l′與直線l交于點P,試判斷![]() 是否為定值,若是請求出定值,若不是請說明理由.
是否為定值,若是請求出定值,若不是請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com