
【題目】已知函數![]() .
.
(Ⅰ)討論![]() 的單調性;
的單調性;
(Ⅱ)設![]() ,證明:當
,證明:當![]() 時,
時,![]() ;
;
(Ⅲ)設![]() 是
是![]() 的兩個零點,證明
的兩個零點,證明![]() .
.
【答案】(Ⅰ)![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;(Ⅱ)當
上單調遞增;(Ⅱ)當![]() 時,
時,![]() ;(Ⅲ)證明過程見解析
;(Ⅲ)證明過程見解析
【解析】試題分析:(Ⅰ)求導,并判斷導數的符號,分別討論![]() 的取值,確定函數的單調區間.
的取值,確定函數的單調區間.
(Ⅱ)構造函數![]() ,利用導數求函數
,利用導數求函數![]() 當
當![]() 時的最大值小于零即可.
時的最大值小于零即可.
(Ⅲ)由(Ⅱ)得![]() ,從而
,從而![]() ,于是
,于是![]() ,由(Ⅰ)知,
,由(Ⅰ)知,![]() .
.
試題解析:(Ⅰ)![]() 的定義域為
的定義域為![]() ,
,
求導數,得![]() ,
,
若![]() ,則
,則![]() ,此時
,此時![]() 在
在![]() 上單調遞增,
上單調遞增,
若![]() ,則由
,則由![]() 得
得![]() ,當
,當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
此時![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
(Ⅱ)令![]() ,則
,則
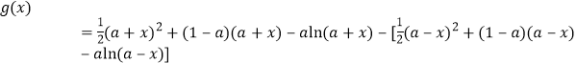
![]() .
.
求導數,得![]() ,
,
當時![]() ,
,![]() ,
,![]() 在
在![]() 上是減函數.
上是減函數.
而![]() ,
,![]() ,
,
故當![]() 時,
時,![]()
(Ⅲ)由(Ⅰ)可知,當![]() 時,函數
時,函數![]() 至多有一個零點,
至多有一個零點,
故![]() ,從而
,從而![]() 的最小值為
的最小值為![]() ,且
,且![]() ,
,
不妨設![]() ,則
,則![]() ,
,![]() ,
,
由(Ⅱ)得![]() ,
,
從而![]() ,于是
,于是![]() ,
,
由(Ⅰ)知,![]() .
.
點晴:本題考查函數導數的單調性.不等式比較大小,函數的零點問題:在(Ⅰ)中通過求導,并判斷導數的符號,分別討論![]() 的取值,確定函數的單調區間.(Ⅱ)通過構造函數
的取值,確定函數的單調區間.(Ⅱ)通過構造函數![]() ,把不等式證明問題轉化為函數求最值問題,求函數
,把不等式證明問題轉化為函數求最值問題,求函數![]() 當
當![]() 時的最大值小于零即可.(Ⅲ)要充分利用(Ⅰ)(Ⅱ)問的結論.
時的最大值小于零即可.(Ⅲ)要充分利用(Ⅰ)(Ⅱ)問的結論.


 活力試卷系列答案
活力試卷系列答案 課課優能力培優100分系列答案
課課優能力培優100分系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() 為自然對數的底數.
為自然對數的底數.
(I)若曲線![]() 在點
在點![]() 處的切線平行于
處的切線平行于![]() 軸,求
軸,求![]() 的值;
的值;
(II)求函數![]() 的極值;
的極值;
(III)當![]() 時,若直線
時,若直線![]() 與曲線
與曲線![]() 沒有公共點,求
沒有公共點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩隊參加聽歌猜歌名游戲,每隊3人.隨機播放一首歌曲,參賽者開始搶答,每人只有一次搶答機會(每人搶答機會均等),答對者為本隊贏得一分,答錯得零分.假設甲隊中每人答對的概率均為 ![]() ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為 ![]() ,
, ![]() ,
, ![]() ,且各人回答正確與否相互之間沒有影響.
,且各人回答正確與否相互之間沒有影響.
(Ⅰ)若比賽前隨機從兩隊的6個選手中抽取兩名選手進行示范,求抽到的兩名選手在同一個隊的概率;
(Ⅱ)用ξ表示甲隊的總得分,求隨機變量ξ的分布列和數學期望;
(Ⅲ)求兩隊得分之和大于4的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x)滿足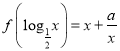 為常數
為常數
(1)求函數f(x)的表達式;
(2)如果f(x)為偶函數,求a的值;
(3)當f(x)為偶函數時,若方程f(x)=m有兩個實數根x1,x2;其中x1<0,0<x2<1;求實數m的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下三個命題 ①設回歸方程為 ![]() =3﹣3x,則變量x增加一個單位時,y平均增加3個單位;
=3﹣3x,則變量x增加一個單位時,y平均增加3個單位;
②兩個隨機變量的線性相關性越強,則相關系數的絕對值越接近于1;
③在某項測量中,測量結果ξ服從正態分布N (1,σ2) (σ>0).若ξ在(0,1)內取值的概率為0.4,則ξ在(0,2)內取值的概率為0.8.
其中真命題的個數為( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)對一切實數x,y均有f(x+y)﹣f(y)=(x+2y+2)x成立,且f(2)=12.
(1)求f(0)的值;
(2)在(1,4)上存在x0∈R,使得f(x0)﹣8=ax0成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古代中國數學輝煌燦爛,在《張丘建算經》中記載:“今有十等人,大官甲等十人官賜金,以等次差降之.上三人先入,得金四斤持出;下四人后入,得金三斤持出;中央三人未到者,亦依等次更給.問:各得金幾何及未到三人復應得金幾何?”則該問題中未到三人共得金多少斤?( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個命題:
①函數y=|x|與函數y=( ![]() )2表示同一個函數;
)2表示同一個函數;
②奇函數的圖象一定通過直角坐標系的原點;
③函數y=3(x﹣1)2的圖象可由y=3x2的圖象向右平移1個單位得到;
④y=2|x|的最小值為1
⑤對于函數f(x),若f(﹣1)f(3)<0,則方程f(x)=0在區間[﹣1,3]上有一實根;
其中正確命題的序號是(填上所有正確命題的序號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com