【題目】如圖，長方體
中，
,點
是
的中點．
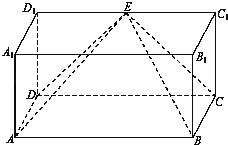
（1）求證：
平面
；
（2）求二面角
的大小．
【答案】（1）證明見解析（2）120°
【解析】
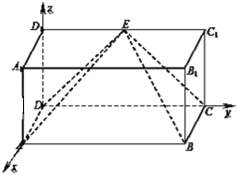
試題（1）建立如圖所示的空間直角坐標(biāo)系，利用向量法能證明DE⊥平面BCE．
（2）求出平面AEB的法向量和平面BCE的法向量，利用向量法能求出二面角A﹣EB﹣C的大小．
（1）證明：建立如圖所示的空間直角坐標(biāo)系，
則D（0，0，0），E（0，1，1），
B（1，2，3），C（0，2，0），
∴
=（0，1，1），
=（﹣1，﹣1，1），
=（﹣1，0，0），
∵
=0，
=0，
∴DE⊥BE，DE⊥BC，
∵BE平面BCE，BC平面BCE，BE∩BC=B，
∴DE⊥平面BCE．
（2）解：設(shè)平面AEB的法向量
=（x，y，z），
則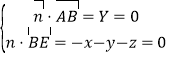
，
取x=1，得=（1，0，1），
∵DE⊥平面BCE，∴
=（0，1，1）是平面BCE的法向量，
∵cos＜
＞=
=
，
∴二面角A﹣EB﹣C的大小為120°．
舉一反三同步巧講精練系列答案
口算與應(yīng)用題卡系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)
（
，且
），
，（其中
為
的導(dǎo)函數(shù)）.
（1）當(dāng)
時，求
的極大值點；
（2）討論
的零點個數(shù).
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，
，
．
（1）求函數(shù)
的極值點；
（2）已知T(
，
)為函數(shù)，
的公共點，且函數(shù)，在點T處的切線相同，求a的值；
（3）若函數(shù)
在(0，
)上的零點個數(shù)為2，求a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)三棱錐
的底面是正三角形，側(cè)棱長均相等，
是棱
上的點（不含端點），記直線
與直線
所成角為
，直線與平面
所成角為
，二面角
的平面角為
，則（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】（1）求與橢圓
有共同焦點且過點
的雙曲線的標(biāo)準(zhǔn)方程；
（2）已知拋物線的焦點在
軸上，拋物線上的點
到焦點的距離等于5，求拋物線的標(biāo)準(zhǔn)方程和
的值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】將集合
中的元素作全排列，使得除了最左端的一個數(shù)之外，對于其余的每個數(shù)
，在的左邊某個位置上總有一個數(shù)與之差的絕對值為1.則滿足條件的排列個數(shù)為____________.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓C：
的右焦點為F(2,0)，過點F的直線交橢圓于M、N兩點且MN的中點坐標(biāo)為
．
（Ⅰ）求橢圓C的方程；
（Ⅱ）設(shè)直線l不經(jīng)過點P（0，b）且與C相交于A，B兩點，若直線PA與直線PB的斜率的和為1，試判斷直線 l是否經(jīng)過定點，若經(jīng)過定點，請求出該定點；若不經(jīng)過定點，請給出理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
