【題目】根據(jù)統(tǒng)計(jì)資料，我國能源生產(chǎn)自1992年以來發(fā)展很快，下面是我國能源生產(chǎn)總量（折合億噸標(biāo)準(zhǔn)煤）的幾個(gè)統(tǒng)計(jì)數(shù)據(jù)：1992年8.6億噸，5年后的1997年10.4億噸，10年后的2002年12.9億噸．有關(guān)專家預(yù)測，到2007年我國能源生產(chǎn)總量將達(dá)到17.1億噸，則專家是依據(jù)下列哪一類函數(shù)作為數(shù)學(xué)模型進(jìn)行預(yù)測的（ ）
A．一次函數(shù) B．二次函數(shù) C．指數(shù)函數(shù) D．對數(shù)函數(shù)
【答案】B
【解析】
試題分析：首先題中數(shù)據(jù)的處理，已知數(shù)據(jù)可看作為
，
，
，估測的是
，如果是一次函數(shù)，可設(shè)函數(shù)為
，把第一、二個(gè)數(shù)據(jù)代入得
，但此時(shí)第三個(gè)數(shù)據(jù)有誤差，第四個(gè)估測的數(shù)據(jù)誤差更大．A不合；如果是二次函數(shù)，設(shè)函數(shù)為
，把三個(gè)數(shù)據(jù)代入可得
，當(dāng)
時(shí)，計(jì)算得
，與估計(jì)值一樣．可以認(rèn)為是用這個(gè)函數(shù)模型預(yù)測的．故選B．
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】為了了解某校學(xué)生喜歡吃辣是否與性別有關(guān)，隨機(jī)對此校100人進(jìn)行調(diào)查，得到如下的列表：已知在全部100人中隨機(jī)抽取1人抽到喜歡吃辣的學(xué)生的概率為
．
喜歡吃辣 | 不喜歡吃辣 | 合計(jì) | |
男生 | 10 | ||
女生 | 20 | ||
合計(jì) | 100 |
（1）請將上面的列表補(bǔ)充完整；
（2）是否有99.9%以上的把握認(rèn)為喜歡吃辣與性別有關(guān)？說明理由：
下面的臨界值表供參考：
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（參考公式：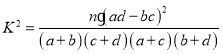
，其中
）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】袋中裝有3個(gè)黑球，4個(gè)白球，從中任取4個(gè)球，則
①至少有1個(gè)白球和至少有1個(gè)黑球； ②至少有2個(gè)白球和恰有3個(gè)黑球；
③至少有1個(gè)黑球和全是白球； ④恰有1個(gè)白球和至多有1個(gè)黑球.
在上述事件中，是互斥事件但不是對立事件的為（ ）
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）=
為定義在R上的奇函數(shù)．
（1）求a，b的值及f（x）的表達(dá)式；
（2）判斷f（x）在定義域上的單調(diào)性并用單調(diào)性的定義證明．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
（
）
（Ⅰ）當(dāng)
時(shí)，求解方程
；
（Ⅱ）根據(jù)
的不同取值，討論函數(shù)的奇偶性，并說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，正四棱錐
中底面邊長為
，側(cè)棱
與底面
所成角的正切值為
．
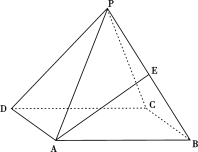
（1）求正四棱錐的外接球半徑；
（2）若E是PB中點(diǎn)，求異面直線PD與AE所成角的正切值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，
（1）若
，求函數(shù)的零點(diǎn)；
（2）若函數(shù)在區(qū)間
上恰有一個(gè)零點(diǎn)，求
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知等比數(shù)列{an}的各項(xiàng)均為正數(shù),且2a1＋3a2＝1, 
．
（Ⅰ）求數(shù)列{an}的通項(xiàng)公式;
（Ⅱ）設(shè)bn＝log3a1＋log3a2＋…＋log3an,求數(shù)列
的前n項(xiàng)和．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖所示,
平面
，四邊形是矩形，
，
分別是
的中點(diǎn)．
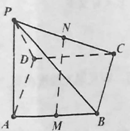
（1）求平面
和平面所成二面角的大小；
（2）求證:
平面；
（3）當(dāng)
的長度變化時(shí), 求異面直線
與
所成角的可能范圍．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com
