【題目】在△ABC中，角A，B，C所對的邊分別為a，b，c，且滿足 
acosC﹣csinA=0．
（1）求角C的大小；
（2）已知b=4，△ABC的面積為6 ，求邊長c的值．
【答案】
（1）解：在△ABC中，由正弦定理得： 
sinAcosC﹣sinCsinA=0． …（2分）
因為0＜A＜π，所以sinA＞0，
從而 cosC=sinC，又cosC≠0，
所以tanC= ，所以C= 
．
（2）解：在△ABC中，S△ABC= 
=6 ，得a=6，
由余弦定理得：c2=62+42﹣2× 
=28，
所以c=2 
【解析】（1）由正弦定理得： sinAcosC﹣sinCsinA=0，即可解得tanC= ，從而求得C的值；（2）由面積公式可得S△ABC= =6 ，從而求得得a的值，由余弦定理即可求c的值．
【考點精析】解答此題的關(guān)鍵在于理解正弦定理的定義的相關(guān)知識，掌握正弦定理:
，以及對余弦定理的定義的理解，了解余弦定理:
;
;
．
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）=x（1+m|x|），關(guān)于x的不等式f（x）＞f（x+m）的解集記為T，若區(qū)間[﹣ 
， ]T，則實數(shù)m的取值范圍是（ ）
A.（ 
，0）
B.（ 
，0）
C.（﹣∞， ）
D.（ ，0）∪（0， ）
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
.
（Ⅰ）若過點
恰有兩條直線與曲線
相切，求
的值；
（Ⅱ）用
表示
中的最小值，設函數(shù)
，若
恰有三個零點，求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系中，圓
與
軸的正半軸交于點
，以
為圓心的圓
與圓
交于
兩點.
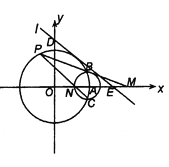
（1）若直線
與圓
切于第一象限，且與坐標軸交于
，當線段
長最小時，求直線
的方程；
（2）設
是圓
上異于
的任意一點，直線
分別與
軸交于點
和
，問
是否為定值？若是，請求出該定值；若不是，請說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】東莞市某高級中學在今年4月份安裝了一批空調(diào)，關(guān)于這批空調(diào)的使用年限
（單位：年， 
）和所支出的維護費用
（單位：萬元）廠家提供的統(tǒng)計資料如下：
（1）請根據(jù)以上數(shù)據(jù)，用最小二乘法原理求出維護費用
關(guān)于
的線性回歸方程
；
（2）若規(guī)定當維護費用
超過13.1萬元時，該批空調(diào)必須報廢，試根據(jù)（1）的結(jié)論預測該批空調(diào)使用年限的最大值.
參考公式：最小二乘估計線性回歸方程
中系數(shù)計算公式：
， 
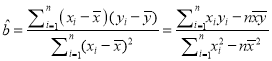，其中
表示樣本均值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
（
），
（
）.
（1）討論
的單調(diào)性；
（2）設
， 
，若
（
）是
的兩個零點，且
，
試問曲線
在點
處的切線能否與
軸平行？請說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
.
（1）求函數(shù)
；
（2）設函數(shù)
，其中a∈(1，2)，求函數(shù)g(x)在區(qū)間[1，e]上的最小值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
