
【題目】已知函數(shù)f(x)= ![]() (k>0).
(k>0).
(1)若f(x)>m的解集為{x|x<﹣3或x>﹣2},求不等式5mx2+ ![]() x+3>0的解集;
x+3>0的解集;
(2)若存在x>3使得f(x)>1成立,求k的取值范圍.
【答案】
(1)解:∵函數(shù)f(x)= ![]() (k>0),f(x)>m的解集為{x|x<﹣3或x>﹣2},
(k>0),f(x)>m的解集為{x|x<﹣3或x>﹣2},
∴f(﹣3)=m,f(﹣2)=m,即 ![]() =m,且
=m,且 ![]() =m,求得k=2,m=﹣
=m,求得k=2,m=﹣ ![]() ,
,
故不等式5mx2+ ![]() x+3>0,即 不等式﹣2x2+x+3>0,即 2x2﹣x﹣3<0,求得﹣1<x<
x+3>0,即 不等式﹣2x2+x+3>0,即 2x2﹣x﹣3<0,求得﹣1<x< ![]() ,
,
故不等式的解集為{x|﹣1<x< ![]() }
}
(2)解:∵存在x>3使得f(x)>1成立,∴ ![]() >1在(3,+∞)上有解,
>1在(3,+∞)上有解,
即x2﹣kx+3k<0在(3,+∞)上有解,k> ![]() 在(3,+∞)上能成立,
在(3,+∞)上能成立,
故k大于g(x)= ![]() 的最小值.
的最小值.
∵g′(x)= ![]() ,∴在(3,6)上,g′(x)<0,g(x)為減函數(shù);
,∴在(3,6)上,g′(x)<0,g(x)為減函數(shù);
在(6,+∞)上,g′(x)>0,g(x)為增函數(shù),故g(x)的最小值為g(6)=12,∴k>12.
【解析】(1)根據(jù)f(x)>m的解集為{x|x<﹣3或x>﹣2},可得 f(﹣3)=m,f(﹣2)=m,求得m、k的值,從而求得不等式5mx2+ ![]() x+3>0的解集.(2)由題意可得k>
x+3>0的解集.(2)由題意可得k> ![]() 在(3,+∞)上能成立,故k大于g(x)=
在(3,+∞)上能成立,故k大于g(x)= ![]() 的最小值.再利用導(dǎo)數(shù)求得g(x)的最小值,可得k的取值范圍.
的最小值.再利用導(dǎo)數(shù)求得g(x)的最小值,可得k的取值范圍.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】《中國詩詞大會》是中央電視臺最近新推出的一檔有重大影響力的大型電視文化節(jié)目,今年兩會期間,教育部部長陳寶生答記者問時給予其高度評價。基于這樣的背景,山東某中學(xué)積極響應(yīng),也舉行了一次詩詞競賽。組委會在競賽后,從中抽取了100名選手的成績(百分制),作為樣本進行統(tǒng)計,作出了圖中的頻率分布直方圖,分析后將得分不低于60分的學(xué)生稱為“詩詞達人”,低于60分的學(xué)生稱為“詩詞待加強者”.

(Ⅰ)根據(jù)已知條件完成下面2×2列聯(lián)表,并據(jù)此判斷是否在犯錯誤的概率不超過0.01的前提下認為“詩詞達人”與性別有關(guān)?
詩詞待加強者 | 詩詞達人 | 合計 | |
男 | 15 | ||
女 | 45 | ||
合計 |
(Ⅱ)將頻率視為概率,現(xiàn)在從該校大量參與活動的學(xué)生中用隨機抽樣的方法每次抽取1人,共抽取3次,記被抽取的3人中“詩詞達人”的人數(shù)為![]() ,若每次抽取的結(jié)果是相互獨立的,求
,若每次抽取的結(jié)果是相互獨立的,求![]() 的分布列、數(shù)學(xué)期望
的分布列、數(shù)學(xué)期望![]() 和方差
和方差![]() .
.
附:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】本著健康、低碳的生活理念,租自行車騎游的人越來越多.某自行車租車點的收費標準是每車每次租時間不超過兩小時免費,超過兩個小時的部分每小時收費2元(不足1小時的部分按1小時計算).有甲、乙兩人獨立來該租車點騎游(各組一車一次).設(shè)甲、乙不超過兩小時還車的概率分別為![]() ,
, ![]() ;兩小時以上且不超過三小時還車的概率分別為
;兩小時以上且不超過三小時還車的概率分別為![]() ,
, ![]() ;兩人租車時間都不會超過四小時.
;兩人租車時間都不會超過四小時.
(1)求甲、乙兩人所付租車費用相同的概率;
(2)設(shè)甲、乙兩人所付的租車費用之和為隨機變量![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)高三年級從甲、乙兩個班級各選出7名學(xué)生參加數(shù)學(xué)競賽,他們?nèi)〉玫某煽儯M分100分)的莖葉圖如圖,其中甲班學(xué)生成績的平均分是85,乙班學(xué)生成績的中位數(shù)是89.
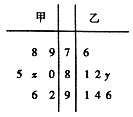
(1)求![]() 和
和![]() 的值;
的值;
(2)計算乙班7位學(xué)生成績的方差![]() .
.
(3)從成績在90分以上的學(xué)生中隨機抽取兩名學(xué)生,求乙班至少有一名學(xué)生的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() 是等腰三角形,
是等腰三角形,![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 上一點.
上一點.
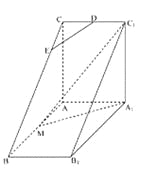
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 將三棱柱
將三棱柱![]() 分成兩個部分,求較小部分與較大部分的體積之比.
分成兩個部分,求較小部分與較大部分的體積之比.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列關(guān)于回歸分析的說法中錯誤的是( )
A. 回歸直線一定過樣本中心![]()
B. 殘差圖中殘差點比較均勻地落在水平的帶狀區(qū)域中,說明選用的模型比較合適
C. 兩個模型中殘差平方和越小的模型擬合的效果越好
D. 甲、乙兩個模型的![]() 分別約為0.98和0.80,則模型乙的擬合效果更好
分別約為0.98和0.80,則模型乙的擬合效果更好
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,內(nèi)角A,B,C所對的邊分別為a,b,c,已知A= ![]() ,b2﹣a2=
,b2﹣a2= ![]() c2 .
c2 .
(1)求tanC的值;
(2)若△ABC的面積為3,求b的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,兩焦點分別為
,兩焦點分別為![]() ,右頂點為
,右頂點為![]() ,
, ![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)設(shè)過定點![]() 的直線
的直線![]() 與雙曲線
與雙曲線![]() 的左支有兩個交點,與橢圓
的左支有兩個交點,與橢圓![]() 交于
交于![]() 兩點,與圓
兩點,與圓![]() 交于
交于![]() 兩點,若
兩點,若![]() 的面積為
的面積為![]() ,
, ![]() ,求正數(shù)
,求正數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
, ![]() 的圖象在點
的圖象在點![]() 處的切線與直線
處的切線與直線![]() 平行.
平行.
(1)求![]() 的值;
的值;
(2)若函數(shù)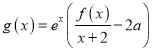 (
(![]() ),且
),且![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)函數(shù),求實數(shù)
上是單調(diào)函數(shù),求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com