
【題目】已知橢圓C以坐標軸為對稱軸,以坐標原點為對稱中心,橢圓的一個焦點為![]() ,點
,點![]() 在橢圓上,
在橢圓上,
![]() Ⅰ
Ⅰ![]() 求橢圓C的方程.
求橢圓C的方程.
![]() Ⅱ
Ⅱ![]() 斜率為k的直線l過點F且不與坐標軸垂直,直線l交橢圓于A、B兩點,線段AB的垂直平分線與x軸交于點G,求點G橫坐標的取值范圍.
斜率為k的直線l過點F且不與坐標軸垂直,直線l交橢圓于A、B兩點,線段AB的垂直平分線與x軸交于點G,求點G橫坐標的取值范圍.
【答案】![]() Ⅰ
Ⅰ![]()
![]() .
.![]() Ⅱ
Ⅱ![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 設橢圓方程為
設橢圓方程為![]() ,由橢圓可得
,由橢圓可得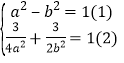 ,解出即可得出.
,解出即可得出.
![]() Ⅱ
Ⅱ![]() 解法一:設
解法一:設![]() ,
,![]() ,AB中點
,AB中點![]() ,直線AB的方程為
,直線AB的方程為![]() ,代入橢圓方程可得
,代入橢圓方程可得![]() ,利用根與系數的關系、中點坐標公式可得N的坐標,可得AB的垂直平分線NG的方程為,進而得出.
,利用根與系數的關系、中點坐標公式可得N的坐標,可得AB的垂直平分線NG的方程為,進而得出.
解法二:設![]() ,
,![]() ,AB中點
,AB中點![]() ,把點A,B的坐標分別代入橢圓方程相減可得:
,把點A,B的坐標分別代入橢圓方程相減可得:![]() ,利用中點坐標公式、斜率計算公式可得斜率
,利用中點坐標公式、斜率計算公式可得斜率![]() ,又
,又![]() ,可得
,可得![]() ,又
,又![]() 在橢圓內,即
在橢圓內,即![]() ,可得
,可得![]() ,利用AB的垂直平分線為
,利用AB的垂直平分線為![]() ,即可得出.
,即可得出.
![]() Ⅰ
Ⅰ![]() 設橢圓方程為
設橢圓方程為![]() ,
,
則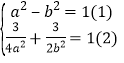
由![]() 得
得![]()
由![]() 得
得![]() 代入
代入![]() 得
得![]() ,
,
即![]() ,即
,即![]() ,或
,或![]()
![]() ,
,![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,
![]() 橢圓方程為
橢圓方程為![]() .
.
![]() Ⅱ
Ⅱ![]() 解法一:設
解法一:設![]() ,
,![]() ,AB中點
,AB中點![]() ,
,
直線AB的方程為![]() ,
,
代入![]() ,整理得
,整理得![]() ,
,
![]() 直線AB過橢圓的左焦點F,
直線AB過橢圓的左焦點F,![]() 方程有兩個不等實根,
方程有兩個不等實根,
則![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 的垂直平分線NG的方程為
的垂直平分線NG的方程為![]() ,
,
![]() 時,
時,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
解法二:設![]() ,
,![]() ,AB中點
,AB中點![]() ,
,
由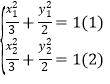 ,
,![]() 得
得![]() ,
,
斜率![]() ,
,
又![]() ,
,![]() ,
,
![]() ,得
,得![]() ,
,
![]() 在橢圓內,即
在橢圓內,即![]() ,
,
將![]() 代入得
代入得![]() ,
,
解得![]()
![]() ,
,
則AB的垂直平分線為![]() ,
,![]() 時,
時,![]() .
.


科目:高中數學 來源: 題型:
【題目】從裝有兩個紅球和兩個黑球的口袋內任取兩個球,那么互斥而不對立的兩個事件是( )
A. “至少有一個黑球”與“都是紅球”
B. “至少有一個黑球”與“至少有一個紅球”
C. “至少有一個黑球”與“都是黑球”
D. “恰有一個黑球”與“恰有兩個黑球”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某學校進行的一次語文與歷史成績中,隨機抽取了25位考生的成績進行分析,25位考生的語文成績已經統計在莖葉圖中,歷史成績如下:
(Ⅰ)請根據數據在莖葉圖中完成歷史成績統計;
(Ⅱ)請根據數據完成語文成績的頻數分布表及語文成績的頻率分布直方圖;
語文成績的頻數分布表:
語文成績分組 | [50,60) | [60,70) | [70,80) | [90,100) | [100,110) | [110,120] |
頻數 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 上一點
上一點![]() 與橢圓右焦點的連線垂直于x軸,直線l:y=kx+m與橢圓C相交于A,B兩點(均不在坐標軸上).
與橢圓右焦點的連線垂直于x軸,直線l:y=kx+m與橢圓C相交于A,B兩點(均不在坐標軸上).
(1)求橢圓C的標準方程;
(2)設O為坐標原點,若△AOB的面積為![]() ,試判斷直線OA與OB的斜率之積是否為定值?若是請求出,若不是請說明理由.
,試判斷直線OA與OB的斜率之積是否為定值?若是請求出,若不是請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓O:![]() 經過點
經過點![]() ,與x軸正半軸交于點B.
,與x軸正半軸交于點B.
![]() Ⅰ
Ⅰ![]() ______;
______;![]() 將結果直接填寫在答題卡的相應位置上
將結果直接填寫在答題卡的相應位置上![]()
![]() Ⅱ
Ⅱ![]() 圓O上是否存在點P,使得
圓O上是否存在點P,使得![]() 的面積為15?若存在,求出點P的坐標;若不存在,說明理由.
的面積為15?若存在,求出點P的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)=2x2+(x﹣2a)|x﹣a|在區間[﹣3,1]上不是單調函數,則實數a的取值范圍是( )
A.[﹣4,1]
B.[﹣3,1]
C.(﹣6,2)
D.(﹣6,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:x0∈[0,2],log2(x+2)<2m;命題q:關于x的方程3x2﹣2x+m2=0有兩個相異實數根.
(1)若(¬p)∧q為真命題,求實數m的取值范圍;
(2)若p∨q為真命題,p∧q為假命題,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com