
【題目】已知函數(shù)![]()
(1)求![]() 的極值;
的極值;
(2)請?zhí)詈孟卤?在答卷),并畫出![]() 的圖象(不必寫出作圖步驟);
的圖象(不必寫出作圖步驟);

(3)設函數(shù)![]() 的圖象與
的圖象與![]() 軸有兩個交點,求
軸有兩個交點,求![]() 的值。
的值。
【答案】(1)見解析(2)當![]() 時
時![]() 有極大值7, 當
有極大值7, 當![]() 時
時![]() 有極小值-20(3)
有極小值-20(3)![]()
【解析】試題分析:(1)求導數(shù)![]() ,解方程
,解方程![]() 求出函數(shù)定義域內(nèi)的所有根;列表檢查
求出函數(shù)定義域內(nèi)的所有根;列表檢查![]() 在
在![]() 的根
的根![]() 左右兩側(cè)值的符號,如果左正右負(左增右減),那么
左右兩側(cè)值的符號,如果左正右負(左增右減),那么![]() 在
在![]() 處取極大值,如果左負右正(左減右增),那么
處取極大值,如果左負右正(左減右增),那么![]() 在
在![]() 處取極小值;(2)直接將表格中數(shù)據(jù)代入解析式,然后描點、連線即可;(3)由(1)知當
處取極小值;(2)直接將表格中數(shù)據(jù)代入解析式,然后描點、連線即可;(3)由(1)知當![]() 時
時![]() 有極大值
有極大值![]() , 當
, 當![]() 時
時![]() 有極小值
有極小值![]() ,可得函數(shù)
,可得函數(shù)![]() 的圖象與
的圖象與![]() 軸有兩個交點時,
軸有兩個交點時, ![]() 或
或![]() .
.
試題解析:(1)![]() ,令
,令![]() 得
得![]() -(2分)
-(2分)
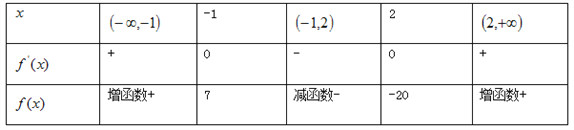
由表知,當![]() 時
時![]() 有極大值7, 當
有極大值7, 當![]() 時
時![]() 有極小值-20.
有極小值-20.
(2)

畫對圖
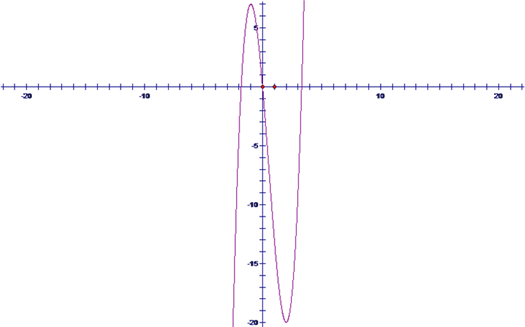
(3)由(1)知當![]() 時
時![]() 有極大值
有極大值![]() , 當
, 當![]() 時
時![]() 有極小值
有極小值![]() ,
,
再由(2)知,當![]() 的極大值或極小值為0時,函數(shù)
的極大值或極小值為0時,函數(shù)![]() 的圖象與
的圖象與![]() 軸有兩個交點,即
軸有兩個交點,即![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】某研究機構對高三學生的記憶力x和判斷力y進行統(tǒng)計分析,得下表數(shù)據(jù):
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)請在圖中畫出上表數(shù)據(jù)的散點圖;

![]() 請根據(jù)上表提供的數(shù)據(jù),用最小二乘法求出y關于x的線性回歸方程
請根據(jù)上表提供的數(shù)據(jù),用最小二乘法求出y關于x的線性回歸方程![]() ;
;
![]() 試根據(jù)
試根據(jù)![]() 求出的線性回歸方程,預測記憶力為9的同學的判斷力.
求出的線性回歸方程,預測記憶力為9的同學的判斷力.
相關公式: .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】隨機擲兩枚質(zhì)地均勻的骰子,它們向上的點數(shù)之和不超過5的概率記為p1,點數(shù)之和大于5的概率記為p2,點數(shù)之和為偶數(shù)的概率記為p3,則
( )
A. p1<p2<p3 B. p2<p1<p3 C. p1<p3<p2 D. p3<p1<p2
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在極坐標系中,已知三點O(0,0),A(2, ![]() ),B(2
),B(2 ![]() ,
, ![]() ).
).
(1)求經(jīng)過O,A,B的圓C1的極坐標方程;
(2)以極點為坐標原點,極軸為x軸的正半軸建立平面直角坐標系,圓C2的參數(shù)方程為 ![]() (θ是參數(shù)),若圓C1與圓C2外切,求實數(shù)a的值.
(θ是參數(shù)),若圓C1與圓C2外切,求實數(shù)a的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知定義在R上的函數(shù)f(x)=x2+|x﹣m|(m為實數(shù))是偶函數(shù),記a=f( ![]() e),b=f(log3π),c=f(em)(e為自然對數(shù)的底數(shù)),則a,b,c的大小關系( )
e),b=f(log3π),c=f(em)(e為自然對數(shù)的底數(shù)),則a,b,c的大小關系( )
A.a<b<c
B.a<c<b
C.c<a<b
D.c<b<a
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】函數(shù)![]() ,且
,且![]() 在
在![]() 處的切線斜率為
處的切線斜率為![]() .
.
(1)求![]() 的值,并討論
的值,并討論![]() 在
在![]() 上的單調(diào)性;
上的單調(diào)性;
(2)設函數(shù)![]()
![]() ,其中
,其中![]() ,若對任意的
,若對任意的![]() 總存在
總存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范圍
的取值范圍
(3)已知函數(shù)![]() ,試判斷
,試判斷![]() 在
在![]() 內(nèi)零點的個數(shù).
內(nèi)零點的個數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某鮮奶店每天以每瓶3元的價格從牧場購進若干瓶鮮牛奶,然后以每瓶7元的價格出售.如果當天賣不完,剩下的鮮牛奶作垃圾處理.
(1)若鮮奶店一天購進30瓶鮮牛奶,求當天的利潤![]() (單位:元)關于當天需求量
(單位:元)關于當天需求量![]() (單位:瓶,
(單位:瓶,![]() )的函數(shù)解析式;
)的函數(shù)解析式;
(2)鮮奶店記錄了100天鮮牛奶的日需求量(單位:瓶),繪制出如下的柱形圖(例如:日需求量為25瓶時,頻數(shù)為5);

(i)若該鮮奶店一天購進30瓶鮮牛奶,求這100天的日利潤(單位:元)的平均數(shù);
(ii) 若該鮮奶店一天購進30瓶鮮牛奶,以100天記錄的各需求量的頻率作為各需求量發(fā)生的概率,求當天的利潤不少于100元的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若函數(shù) ![]() 的圖象向左平移
的圖象向左平移 ![]() 個單位,得到的函數(shù)圖象的對稱中心與f(x)圖象的對稱中心重合,則ω的最小值是( )
個單位,得到的函數(shù)圖象的對稱中心與f(x)圖象的對稱中心重合,則ω的最小值是( )
A.1
B.2
C.4
D.8
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】公差不為零的等差數(shù)列{an}中,a1 , a2 , a5成等比數(shù)列,且該數(shù)列的前10項和為100,數(shù)列{bn}的前n項和為Sn , 且滿足Sn= ![]() ,n∈N* .
,n∈N* .
(1)求數(shù)列{an},{bn}的通項公式;
(2)記得數(shù)列{ ![]() }的前n項和為Tn , 求Tn的取值范圍.
}的前n項和為Tn , 求Tn的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com