
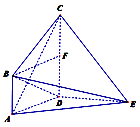
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
(1)求證:![]() ;
;
(2)當(dāng)幾何體![]() 的體積等于
的體積等于![]() 時,求四棱錐.
時,求四棱錐.![]() 的側(cè)面積.
的側(cè)面積.

【答案】(1)見解析;(2)![]() .
.
【解析】
試題分析:(1)取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連結(jié)
,連結(jié)![]() ,由直角梯形
,由直角梯形![]() 性質(zhì)可得
性質(zhì)可得![]()
![]() ,又
,又![]()
![]() 平面
平面![]() ;(2)由
;(2)由![]() 可得
可得 ![]() ,根據(jù)(1)可得三角形
,根據(jù)(1)可得三角形![]() 是直角三角形,根據(jù)勾股定理可得其他三個側(cè)面也是直角三角形,由三角形面積公式可得 四棱錐.
是直角三角形,根據(jù)勾股定理可得其他三個側(cè)面也是直角三角形,由三角形面積公式可得 四棱錐.![]() 的側(cè)面積.
的側(cè)面積.
試題解析:(1)取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連結(jié)
,連結(jié)![]() ,
,
則直角梯形![]() 中,
中,![]() ,
,![]()
![]() 即:
即:![]()
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
又![]()
![]()
(2)![]()
![]()
![]()
![]() ,
,![]() ,
,
又![]()
![]()
![]()
![]() 四棱錐
四棱錐![]() 的側(cè)面積為
的側(cè)面積為
![]() .
.
【方法點(diǎn)晴】本題主要考查線面垂直、棱錐的側(cè)面積及“等積變換”的應(yīng)用,屬于難題.證明直線和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推論![]() ;(3)利用面面平行的性質(zhì)
;(3)利用面面平行的性質(zhì)![]() ;(4)利用面面垂直的性質(zhì),當(dāng)兩個平面垂直時,在一個平面內(nèi)垂直于交線的直線垂直于另一個平面.
;(4)利用面面垂直的性質(zhì),當(dāng)兩個平面垂直時,在一個平面內(nèi)垂直于交線的直線垂直于另一個平面.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】學(xué)校藝術(shù)節(jié)對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項(xiàng)參賽作品,只評一項(xiàng)一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學(xué)對這四項(xiàng)參賽作品預(yù)測如下:
四項(xiàng)參賽作品,只評一項(xiàng)一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學(xué)對這四項(xiàng)參賽作品預(yù)測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項(xiàng)作品未獲得一等獎”;
兩項(xiàng)作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學(xué)中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】科學(xué)研究表明:人類對聲音有不的感覺,這與聲音的強(qiáng)度![]() 單位:瓦
單位:瓦![]() 平方米
平方米![]() 有關(guān)
有關(guān)![]() 在實(shí)際測量時,常用
在實(shí)際測量時,常用![]() 單位:分貝
單位:分貝![]() 來表示聲音強(qiáng)弱的等級,它與聲音的強(qiáng)度I滿足關(guān)系式:
來表示聲音強(qiáng)弱的等級,它與聲音的強(qiáng)度I滿足關(guān)系式:![]() 是常數(shù)
是常數(shù)![]() ,其中
,其中![]() 瓦
瓦![]() 平方米
平方米![]() 如風(fēng)吹落葉沙沙聲的強(qiáng)度
如風(fēng)吹落葉沙沙聲的強(qiáng)度![]() 瓦
瓦![]() 平方米,它的強(qiáng)弱等級
平方米,它的強(qiáng)弱等級![]() 分貝.
分貝.
![]() 已知生活中幾種聲音的強(qiáng)度如表:
已知生活中幾種聲音的強(qiáng)度如表:
聲音來源
聲音大小 | 風(fēng)吹落葉沙沙聲 | 輕聲耳語 | 很嘈雜的馬路 |
強(qiáng)度 |
|
|
|
強(qiáng)弱等級 | 10 | m | 90 |
求a和m的值
![]() 為了不影響正常的休息和睡眠,聲音的強(qiáng)弱等級一般不能超過50分貝,求此時聲音強(qiáng)度I的最大值.
為了不影響正常的休息和睡眠,聲音的強(qiáng)弱等級一般不能超過50分貝,求此時聲音強(qiáng)度I的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(1)求證:![]()
(2)若函數(shù)![]() 的圖象與直線
的圖象與直線![]() 沒有交點(diǎn),求實(shí)數(shù)
沒有交點(diǎn),求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)若函數(shù)![]() ,則是否存在實(shí)數(shù)
,則是否存在實(shí)數(shù)![]() ,使得
,使得![]() 的最小值為
的最小值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)![]() ,
,![]() 是函數(shù)
是函數(shù)![]() (
(![]() ,
,![]() )圖象上的任意兩點(diǎn),且角
)圖象上的任意兩點(diǎn),且角![]() 的終邊經(jīng)過點(diǎn)
的終邊經(jīng)過點(diǎn)![]() ,若
,若![]() 時,
時,![]() 的最小值為
的最小值為![]() .
.
(1)求函數(shù)![]() 的解析式;
的解析式;
(2)當(dāng)![]() 時,不等式
時,不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】類比平面幾何中的定理:△ABC中,若DE是△ABC的中位線,則有S△ADE∶S△ABC=1∶4;若三棱錐A-BCD有中截面EFG∥平面BCD,則截得三棱錐的體積與原三棱錐體積之間的關(guān)系式為________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)”是“函數(shù)
上單調(diào)”是“函數(shù)![]() 在
在![]() 上有反函數(shù)”的( )
上有反函數(shù)”的( )
A.充分不必要條件B.必要不充分條件
C.充分必要條件D.既不充分又不必要條件
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=x2+2﹣alnx﹣bx(a>0).
(Ⅰ)若a=1,b=3,求函數(shù)y=f(x)在(1,f(1))處的切線方程;
(Ⅱ)若f(x1)=f(x2)=0,且x1≠x2,證明:f′(![]() )>0.
)>0.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com