
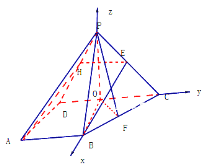
【題目】已知在四棱錐![]() 中,
中,![]() ,
,![]() ,E為PC的中點,
,E為PC的中點,![]() ,
,![]()

(1)求證:![]()
(2)若![]() 與面ABCD所成角為
與面ABCD所成角為![]() ,P在面ABCD射影為O,問是否在BC上存在一點F,使面
,P在面ABCD射影為O,問是否在BC上存在一點F,使面![]() 與面PAB所成的角為
與面PAB所成的角為![]() ,若存在,試求點F的位置,不存在,請說明理由.
,若存在,試求點F的位置,不存在,請說明理由.
【答案】(1)見解析 (2)當F為BC的中點時,兩平面所成的角為![]() .
.
【解析】
(1)連接![]() ,取
,取![]() 的中點
的中點![]() ,連接
,連接![]() ,通過證明
,通過證明![]() 為平行四邊形,得到
為平行四邊形,得到![]() ,根據線面垂直判定定理即可得結論;(2)作
,根據線面垂直判定定理即可得結論;(2)作![]() ,結合可知
,結合可知![]() 為
為![]() 點在面
點在面![]() 的射影,
的射影,![]() ,以
,以![]() 為坐標原點,分別以
為坐標原點,分別以![]() ,
,![]() ,
,![]() 為
為![]() ,
,![]() ,
,![]() 軸,建立空間直角坐標系,設
軸,建立空間直角坐標系,設![]() ,求出面
,求出面![]() 和面
和面![]() 分別為
分別為![]() 和
和![]() ,結合夾角為
,結合夾角為![]() ,求出
,求出![]() 即可.
即可.
(1)證明:

連接BE,取PD的中點H,連接AH,則![]() 又
又![]() ,
,![]()
可知![]() 且
且![]() ,可知ABEH為平行四邊形,故
,可知ABEH為平行四邊形,故![]() ,所以
,所以![]() .
.
(2)![]() 面
面![]()
![]() 面
面![]() ,
,![]() ,作
,作![]() ,可知
,可知![]() 為
為![]() 點在面
點在面![]() 的射影,
的射影,![]() ,以
,以![]() 為坐標原點,分別以
為坐標原點,分別以![]() ,
,![]() ,
,![]() 為
為![]() ,
,![]() ,
,![]() 軸,建立空間直角坐標系
軸,建立空間直角坐標系![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
由![]() 可知
可知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
設![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,可知
,可知![]() ,
,
設面![]() 的法向量為
的法向量為![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
設面POF的法向量為![]() ,
,![]() ,可知
,可知![]() ,可知
,可知![]() ,可知
,可知
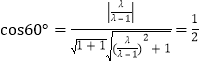 ,解得
,解得![]() ,可知當F為BC的中點時,兩平面所成的角為
,可知當F為BC的中點時,兩平面所成的角為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知圓C過點M(0,-2)、N(3,1),且圓心C在直線x+2y+1=0上.
(1)求圓C的方程;
(2)設直線ax-y+1=0與圓C交于A,B兩點,是否存在實數a,使得過點P(2,0)的直線l垂直平分弦AB?若存在,求出實數a的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,四邊形
中,四邊形![]() 是邊長為2的正方形,
是邊長為2的正方形,![]() ,
,![]() 為
為![]() 的中點,點
的中點,點![]() 在
在![]() 上,
上,![]() 平面
平面![]() ,
,![]() 在
在![]() 的延長線上,且
的延長線上,且![]() .
.
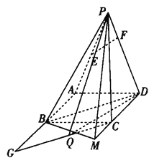
(1)證明:![]() 平面
平面![]() .
.
(2)過點![]() 作
作![]() 的平行線,與直線
的平行線,與直線![]() 相交于點
相交于點![]() ,點
,點![]() 為
為![]() 的中點,求
的中點,求![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】幻彩摩天輪位于中山市西區興中廣場C段4層高的建筑之上,與中山市第一家四星級酒店——富華酒店隔河相望,其外觀是參考世界最高的摩天輪新加坡“飛行者”的設計,輪體上有36個吊艙,共可同時承載288人從高空俯瞰岐江一河兩岸的美景.幻彩摩天輪直徑為83m,每20min轉一圈,最高點離地108m,摩天輪上的點P的起始位置在最低點處.已知在時刻t(min)時P距離地面的高度![]() ,(其中
,(其中![]() ),
),
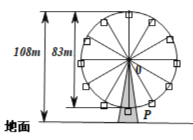
(1)求![]() 的函數解析式.
的函數解析式.
(2)當離地面![]() m以上時,可以俯瞰富華酒店頂樓,求轉一圈中有多少時間可以俯瞰富華酒店頂樓?
m以上時,可以俯瞰富華酒店頂樓,求轉一圈中有多少時間可以俯瞰富華酒店頂樓?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com