
【題目】設x取實數,則f(x)與g(x)表示同一個函數的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)= ![]() ,g(x)=
,g(x)= ![]()
C.f(x)=1,g(x)=(x﹣1)0
D.f(x)= ![]() ,g(x)=x﹣3
,g(x)=x﹣3
【答案】B
【解析】解:A組中兩函數的定義域相同,對應關系不同,g(x)=|x|≠x,故A中的兩函數不為同一個函數;B組中兩函數的定義域均為所有正數構成的集合,對應關系化簡為f(x)=g(x)=1,故B中的兩函數是同一個函數;
C組中兩函數的定義域不同,f(x)的定義域為R,g(x)的定義域為{x|x≠1},故C中的兩函數不為同一個函數;
D組中兩函數的定義域不同,g(x)的定義域為R,f(x)的定義域由不等于﹣3的實數構成,故D中的兩函數不為同一個函數.
故選B.
根據確定函數的三要素判斷每組函數是否為同一個函數,即需要確定每組函數的定義域、對應關系、值域是否相同,也可只判斷前兩項是否相同即可確定這兩個函數是否為同一個函數.


科目:高中數學 來源: 題型:
【題目】盒內有大小相同的9個球,其中2個紅色球,3個白色球,4個黑色球.規定取出1個紅色球得1分,取出1個白色球得0分,取出1個黑色球得![]() 分,現從盒內任取3個球.
分,現從盒內任取3個球.
(Ⅰ)求取出的3個球中至少有一個紅球的概率;
(Ⅱ)求取出的3個球得分之和恰為1分的概率;
(Ⅲ)設![]() 為取出的3個球中白色球的個數,求
為取出的3個球中白色球的個數,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某天數學課上,你突然驚醒,發現黑板上有如下內容:
例:求x3﹣3x,x∈[0,+∞)的最小值.解:利用基本不等式a+b+c≥3 ![]() ,得到x3+1+1≥3x,于是x3﹣3x=x3+1+1﹣3x﹣2≥3x﹣3x﹣2=﹣2,當且僅當x=1時,取到最小值﹣2
,得到x3+1+1≥3x,于是x3﹣3x=x3+1+1﹣3x﹣2≥3x﹣3x﹣2=﹣2,當且僅當x=1時,取到最小值﹣2
(1)老師請你模仿例題,研究x4﹣4x,x∈[0,+∞)上的最小值;
(提示:a+b+c+d≥4 ![]() )
)
(2)研究 ![]() x3﹣3x,x∈[0,+∞)上的最小值;
x3﹣3x,x∈[0,+∞)上的最小值;
(3)求出當a>0時,x3﹣ax,x∈[0,+∞)的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]()
(1)求證f(x)在(0,+∞)上遞增
(2)若f(x)在[m,n]上的值域是[m,n],求實數a的取值范圍
(3)當f(x)≤2x在(0,+∞)上恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
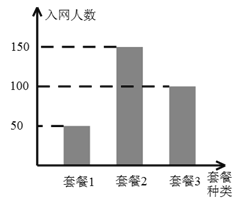
【題目】移動公司在春節正月初八這天推出4G套餐,對這天辦理套餐的客戶進行優惠,優惠方案如下:選擇套餐一的客戶可獲得優惠200元,選擇套餐二的客戶可獲得優惠500元,選擇套餐三的客戶可獲得優惠300元. 初八當天參與活動的人數統計結果如圖所示,
(Ⅰ)從參加當天活動的人中任選一人,求此人獲得優惠金額不低于300元的概率(將頻率視為概率);
(Ⅱ)若采用分層抽樣的方式從參加活動的客戶中選出6人,再從該6人中隨機選兩人,求這兩人獲得相等優惠金額的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com