
【題目】如圖為我國數學家趙爽(約3世紀初)在為《周牌算經》作注時驗證勾股定理的示意圖,現在提供6種不同的顏色給其中5個小區域涂色,規定每個區域只涂一種顏色,相鄰區域顏色不同,則![]() ,
,![]() 區域涂同色的概率為( )
區域涂同色的概率為( )
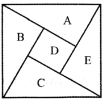
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
本題從顏色使用數量上來分類,又由條件知至少使用三種顏色,所以只剩三種情況了.然后選色,再按照規定每個區域只涂一種顏色,相鄰區域顏色不同,使用分步計數原理逐一涂色,即可求出總的基本事件,再弄清![]() ,
,![]() 區域涂同色的占了多少個基本事件,利用古典概型及其概率計算公式求答案.
區域涂同色的占了多少個基本事件,利用古典概型及其概率計算公式求答案.
解:根據題意,至少使用3種顏色.由使用顏色數量,下面我們分三種情況:
(1)使用5種顏色:選色![]() ,涂上去
,涂上去![]() ,共有
,共有![]() 種;
種;
(2)使用4種顏色:選色![]() ,先涂
,先涂![]() 有4種,下面,①、若
有4種,下面,①、若![]() 、
、![]() 同色,則
同色,則![]() 和
和![]() 各涂剩余的兩色,有
各涂剩余的兩色,有![]() 種,②、若
種,②、若![]() 、
、![]() 不同色,則
不同色,則![]() 和
和![]() 必同色,有
必同色,有![]() 種.
種.![]() 共
共![]() 種;
種;
(3)使用3種顏色:選色![]() ,先涂
,先涂![]() 有3種選擇,
有3種選擇,![]() 用掉一種顏色,下面只有
用掉一種顏色,下面只有![]() 、
、![]() 同色,
同色,![]() 、
、![]() 同色,有
同色,有![]() 種,共
種,共![]() 種,
種,
![]() 共計
共計![]() 種,
種,
其中![]() ,
,![]() 區域涂同色的有
區域涂同色的有![]() 種,
種,
則![]() ,
,![]() 區域涂同色的概率為
區域涂同色的概率為![]() .
.
故選:![]() .
.


 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】為了解貴州省某州2020屆高三理科生的化學成績的情況,該州教育局組織高三理科生進行了摸底考試,現從參加考試的學生中隨機抽取了100名理科生,,將他們的化學成績(滿分為100分)分為![]()
![]()
![]()
![]()
![]()
![]() 6組,得到如圖所示的頻率分布直方圖.
6組,得到如圖所示的頻率分布直方圖.
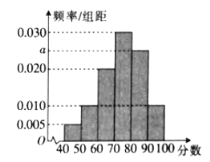
(1)求a的值;
(2)記A表示事件“從參加考試的所有理科生中隨機抽取一名學生,該學生的化學成績不低于70分”,試估計事件A發生的概率;
(3)在抽取的100名理科生中,采用分層抽樣的方法從成績在![]() 內的學生中抽取10名,再從這10名學生中隨機抽取4名,記這4名理科生成績在
內的學生中抽取10名,再從這10名學生中隨機抽取4名,記這4名理科生成績在![]() 內的人數為X,求X的分布列與數學期望.
內的人數為X,求X的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為提高生產效率,開展技術創新活動,提出了完成某項生產任務的兩種新的生產方式.為比較兩種生產方式的效率,選取40名工人,將他們隨機分成兩組,每組20人,第一組工人用第一種生產方式,第二組工人用第二種生產方式.根據工人完成生產任務的工作時間(單位:min)繪制了如下莖葉圖:

(1)根據莖葉圖判斷哪種生產方式的效率更高?并說明理由;
(2)求40名工人完成生產任務所需時間的中位數![]() ,并將完成生產任務所需時間超過
,并將完成生產任務所需時間超過![]() 和不超過
和不超過![]() 的工人數填入下面的列聯表:
的工人數填入下面的列聯表:
超過 | 不超過 | |
第一種生產方式 | ||
第二種生產方式 |
(3)根據(2)中的列聯表,能否有99%的把握認為兩種生產方式的效率有差異?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古希臘時期,人們認為最美人體的頭頂至肚臍的長度與肚臍至足底的長度之比是![]() (
(![]() ≈0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是
≈0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是![]() .若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26 cm,則其身高可能是
.若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26 cm,則其身高可能是

A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】動點![]() 到
到![]() 距離與到直線
距離與到直線![]() 的距離之比為
的距離之比為![]() ,記動點
,記動點![]() 的軌跡為
的軌跡為![]() .
.
(1)求出曲線![]() 的方程,并求出
的方程,并求出![]() 的最小值,其中點
的最小值,其中點![]()
(2)![]() 是曲線
是曲線![]() 上的動點,且直線
上的動點,且直線![]() 經過定點
經過定點![]() ,問在
,問在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() ,若存在,請求出定點
,若存在,請求出定點![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com