
【題目】已知函數f(x)=exlnx(x>0),若對 ![]() 使得方程f(x)=k有解,則實數a的取值范圍是( )
使得方程f(x)=k有解,則實數a的取值范圍是( )
A.(0,ee]
B.[ee , +∞)
C.[e,+∞)
D.![]()
 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案 小學學習好幫手系列答案
小學學習好幫手系列答案科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準x(噸),一位居民的月用水量不超過x的部分按平價收費,超出x的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5)分成9組,制成了如圖所示的頻率分布直方圖. 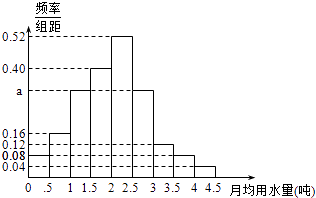
(Ⅰ)求直方圖中a的值;
(Ⅱ)設該市有30萬居民,估計全市居民中月均用水量不低于3噸的人數,并說明理由;
(Ⅲ)若該市政府希望使85%的居民每月的用水量不超過標準x(噸),估計x的值,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究某高校大學5000名新生的視力情況,隨機地抽查了該校100名進校新生的視力情況,得到其頻率分布直方圖如右圖,若規定視力低于5.0的學生屬[于近視學生,則估計該校新生中不是近視的人數約為( )
A.300人
B.400人
C.600人
D.1000人
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的前n項和為Sn , 且a3=3,S7=28,在等比數列{bn}中,b3=4,b4=8.
(1)求an及bn;
(2)設數列{anbn}的前n項和為Tn , 求Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知邊長為1的正方形 ![]() 與
與 ![]() 所在的平面互相垂直,點
所在的平面互相垂直,點 ![]() 分別是線段
分別是線段 ![]() 上的動點(包括端點),
上的動點(包括端點), ![]() ,設線段
,設線段 ![]() 的中點的軌跡為
的中點的軌跡為 ![]() ,則
,則 ![]() 的長度為( )
的長度為( )
A.![]()
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在梯形ABCD中,∠ADC= ![]() ,AB∥CD,PC⊥平面ABCD,CP=AB=2DC=2DA,點E在BP上,且EB=2PE.
,AB∥CD,PC⊥平面ABCD,CP=AB=2DC=2DA,點E在BP上,且EB=2PE. 
(1)求證:DP∥平面ACE;
(2)求二面角E﹣AC﹣P的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=ax3﹣x2﹣x+b(a,b∈R,a≠0),g(x)= ![]() (e是自然對數的底數),f(x)的圖象在x=﹣
(e是自然對數的底數),f(x)的圖象在x=﹣ ![]() 處的切線方程為y=
處的切線方程為y= ![]() .
.
(1)求a,b的值;
(2)探究直線y= ![]() .是否可以與函數g(x)的圖象相切?若可以,寫出切點的坐標,否則,說明理由;
.是否可以與函數g(x)的圖象相切?若可以,寫出切點的坐標,否則,說明理由;
(3)證明:當x∈(﹣∞,2]時,f(x)≤g(x).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com