【題目】已知函數
．
（1）記
的極小值為
，求的最大值；
（2）若對任意實數
恒有
，求
的取值范圍．
科目：高中數學 來源： 題型：
【題目】三國魏人劉徽，自撰《海島算經》，專論測高望遠．其中有一題：今有望海島，立兩表齊，高三丈，前後相去千步，令後表與前表相直。從前表卻行一百二十三步，人目著地取望島峰，與表末參合。從後表卻行百二十七步，人目著地取望島峰，亦與表末參合。問島高及去表各幾何?翻譯如下：要測量海島上一座山峰
的高度
，立兩根高三丈的標桿
和
，前后兩竿相距
步，使后標桿桿腳
與前標桿桿腳
與山峰腳
在同一直線上，從前標桿桿腳退行
步到
，人眼著地觀測到島峰，、
、
、三點共線，從后標桿桿腳退行
步到
，人眼著地觀測到島峰，、
、三點也共線，則山峰的高度
__________步．（古制
步
尺，里
丈
尺
步）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
．
（1）求函數
的極值；
（2）對于曲線上的不同兩點
，如果存在曲線上的點
，且
使得曲線在點
處的切線
，則稱
為弦
的伴隨直線，特別地，當
時，又稱為的
—伴隨直線．
①求證：曲線
的任意一條弦均有伴隨直線，并且伴隨直線是唯一的；
②是否存在曲線
，使得曲線的任意一條弦均有
—伴隨直線？若存在，給出一條這樣的曲線，并證明你的結論；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某研究性學習小組對春季晝夜溫差大小與某花卉種子發芽多少之間的關系進行研究，他們分別記錄了3月1日至3月5日的每天晝夜溫差
與實驗室每天每100顆種子浸泡后的發芽數
，作了初步處理，得到下表：
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
溫差 | 10 | 11 | 13 | 12 | 9 |
發芽率 | 23 | 25 | 30 | 26 | 16 |
（1）從3月1日至3月5日中任選2天，記發芽的種子數分別為
，求事件“均小于26”的概率；
（2）請根據3月1日至3月5日的數據，求出
關于
的線性回歸方程
，并預報3月份晝夜溫差為14度時實驗室每天100顆種子浸泡后的發芽（取整數值）．
附：回歸方程中的斜率和截距最小二乘法估計公式分別為：
，
，
，
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某大學開設甲、乙、丙三門選修課，學生是否選修哪門課互不影響，已知某學生只選修甲的概率為0.08，只選修甲和乙的概率是0.12，至少選修一門的概率是0.88，用
表示該學生選修的課程門數和沒有選修的課程門數的乘積．
（1）記“函數
為
上的偶函數”為事件
，求事件
的概率；
（2）求
的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某投資公司擬投資開發某項新產品，市場評估能獲得10～1 000萬元的投資收益．現公司準備制定一個對科研課題組的獎勵方案：獎金y(單位：萬元)隨投資收益x(單位：萬元)的增加而增加，且獎金不低于1萬元，同時不超過投資收益的20%.
(1) 設獎勵方案的函數模型為f(x)，試用數學語言表述公司對獎勵方案的函數模型f(x)的基本要求；
(2) 公司能不能用函數f(x)＝
＋2作為預設的獎勵方案的模型函數？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，游客從某旅游景區的景點
處下上至
處有兩種路徑．一種是從
沿直線步行到
，另一種是先從
沿索道乘纜車到
，然后從
沿直線步行到
．現有甲、乙兩位游客從
處下山，甲沿
勻速步行，速度為
．在甲出發
后，乙從
乘纜車到
，在
處停留
后，再從
勻速步行到
，假設纜車勻速直線運動的速度為
，山路
長為1260
，經測量
，
．
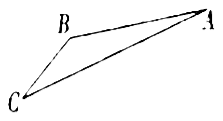
（1）求索道
的長；
（2）問：乙出發多少
后，乙在纜車上與甲的距離最短？
（3）為使兩位游客在
處互相等待的時間不超過
，乙步行的速度應控制在什么范圍內？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
