
【題目】(題文)已知函數![]() ,其中
,其中![]() 為正實數.
為正實數.
(1)若函數![]() 在
在![]() 處的切線斜率為2,求
處的切線斜率為2,求![]() 的值;
的值;
(2)求函數![]() 的單調區間;
的單調區間;
(3)若函數![]() 有兩個極值點
有兩個極值點![]() ,求證:
,求證:![]()
【答案】(1)1;(2)見解析;(3)見解析
【解析】試題分析:(1)根據導數幾何意義得![]() ,解得
,解得![]() 的值;(2)先求導數,再根據導函數是否變號分類討論,最后根據導函數符號確定單調區間(3)先根據韋達定理得
的值;(2)先求導數,再根據導函數是否變號分類討論,最后根據導函數符號確定單調區間(3)先根據韋達定理得![]() ,再化簡
,再化簡![]() ,進而化簡所證不等式為
,進而化簡所證不等式為![]() ,最后利用導函數求函數
,最后利用導函數求函數![]() 單調性,進而確定最小值,證得結論
單調性,進而確定最小值,證得結論
試題解析:(1)因為![]() ,所以
,所以![]() ,
,
則![]() ,所以
,所以![]() 的值為1.
的值為1.
(2) ![]() ,函數
,函數![]() 的定義域為
的定義域為![]() ,
,
![]() 若
若![]() ,即
,即![]() ,則
,則![]() ,此時
,此時![]() 的單調減區間為
的單調減區間為![]() ;
;
![]() 若
若![]() ,即
,即![]() ,則
,則![]() 的兩根為
的兩根為![]() ,
,
此時![]() 的單調減區間為
的單調減區間為![]() ,
,![]() ,
,
單調減區間為![]() .
.
(3)由(2)知,當![]() 時,函數
時,函數![]() 有兩個極值點
有兩個極值點![]() ,且
,且![]() .
.
因為![]()
![]()
![]()
要證![]() ,只需證
,只需證![]() .
.
構造函數![]() ,則
,則![]() ,
,
![]() 在
在![]() 上單調遞增,又
上單調遞增,又![]() ,且
,且![]() 在定義域上不間斷,
在定義域上不間斷,
由零點存在定理,可知![]() 在
在![]() 上唯一實根
上唯一實根![]() , 且
, 且![]() .
.
則![]() 在
在![]() 上遞減,
上遞減, ![]() 上遞增,所以
上遞增,所以![]() 的最小值為
的最小值為![]() .
.
因為![]() ,
,
當![]() 時,
時, ![]() ,則
,則![]() ,所以
,所以![]() 恒成立.
恒成立.
所以![]() ,所以
,所以![]() ,得證.
,得證.


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,點M(1,0)與橢圓短軸的兩個端點的連線相互垂直.
,點M(1,0)與橢圓短軸的兩個端點的連線相互垂直.
(1)求橢圓C的方程;
(2)過點M(1,0)的直線與橢圓C相交于A、B兩點,設點N(3,2),記直線AN、BN的斜率分別為k1、k2,求證:k1+k2為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個袋子中有5個大小相同的球,其中3個白球與2個黑球,現從袋中任意取出一個球,取出后不放回,然后再從袋中任意取出一個球,則第一次為白球、第二次為黑球的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,以坐標原點為極點,以![]() 軸正半軸為極軸,建立極坐標系,點
軸正半軸為極軸,建立極坐標系,點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() ,且
,且![]() 過點
過點![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為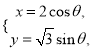 (
(![]() 為參數).
為參數).
(Ⅰ)求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最大值;
的距離的最大值;
(Ⅱ)過點![]() 與直線
與直線![]() 平行的直線
平行的直線![]() 與曲線
與曲線 ![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下兩個圖表是2019年初的4個月我國四大城市的居民消費價格指數(上一年同月![]() )變化圖表,則以下說法錯誤的是( )
)變化圖表,則以下說法錯誤的是( )
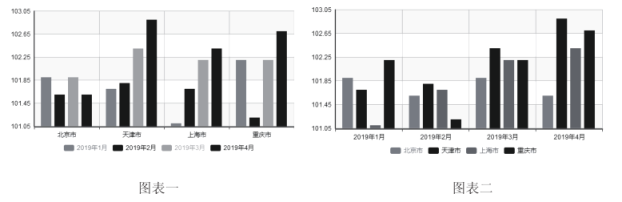
(注:圖表一每個城市的條形圖從左到右依次是1、2、3、4月份;圖表二每個月份的條形圖從左到右四個城市依次是北京、天津、上海、重慶)
A.3月份四個城市之間的居民消費價格指數與其它月份相比增長幅度較為平均
B.4月份僅有三個城市居民消費價格指數超過102
C.四個月的數據顯示北京市的居民消費價格指數增長幅度波動較小
D.僅有天津市從年初開始居民消費價格指數的增長呈上升趨勢
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某親子公園擬建議廣告牌,將邊長為![]() 米的正方形ABCD和邊長為1米的正方形AEFG在A點處焊接,AM、AN、GM、DN均用加強鋼管支撐,其中支撐鋼管GM、DN垂直于地面于M點和N點,且GM、DN、MN長度相等
米的正方形ABCD和邊長為1米的正方形AEFG在A點處焊接,AM、AN、GM、DN均用加強鋼管支撐,其中支撐鋼管GM、DN垂直于地面于M點和N點,且GM、DN、MN長度相等![]() 不計焊接點大小
不計焊接點大小![]()

![]() 若
若![]() 時,求焊接點A離地面距離;
時,求焊接點A離地面距離;
![]() 若記
若記![]() ,求加強鋼管AN最長為多少?
,求加強鋼管AN最長為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
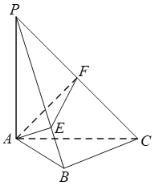
【題目】在《九章算術》中,將四個面都為直角三角形的四面體稱之為鱉臑.如圖,在鱉臑![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,過點
,過點![]() 分別作
分別作![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,連結
,連結![]() ,當
,當![]() 的面積最大時,
的面積最大時,![]() __________.
__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的離心率為
的離心率為![]() ,過橢圓右焦點
,過橢圓右焦點![]() 作兩條互相垂直的弦
作兩條互相垂直的弦![]() 與
與![]() .當直線
.當直線![]() 的斜率為0時,
的斜率為0時,![]() .
.
(1)求橢圓的方程;
(2)試探究![]() 是否為定值?若是,證明你的結論;若不是,請說明理由.
是否為定值?若是,證明你的結論;若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com