【題目】已知A，B，C為△ABC的三個內(nèi)角，且其對邊分別為a，b，c，若c2+b2+cb=a2
（1）求A；
（2）若a=2 
，b+c=4，求△ABC的面積．
【答案】
（1）解：在△ABC中，∵c2+b2+cb=a2，∴c2+b2﹣a2=﹣bc，
∴由余弦定理可得：cosA= 
= 
=﹣ 
，
∵A∈（0，π），
∴A= 
（2）解：∵由（1）可知：cosA= = 
=﹣ ，
又∵a=2 
，b+c=4，
∴ 
=﹣ ，解得：bc=4，
∴△ABC的面積S= bcsinA= 
=
【解析】（1）由已知可得c2+b2﹣a2=﹣bc，利用余弦定理可得cosA=﹣ ，結(jié)合范圍A∈（0，π），可求A的值．（2）由（1）可知cosA= =﹣ ，從而可求bc的值，利用三角形面積公式即可計算得解．
【考點精析】本題主要考查了正弦定理的定義和余弦定理的定義的相關(guān)知識點，需要掌握正弦定理:
；余弦定理:
;
;
才能正確解答此題．
閱讀快車系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù) 
（1）求f（x）的單調(diào)區(qū)間；
（2）求曲線y=f（x）在點（1，f（1））處的切線方程；
（3）求證：對任意的正數(shù)a與b，恒有 
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）= 
ax2+4x﹣lnx．
（1）當(dāng)a=﹣3時，求f（x）的單調(diào)區(qū)間；
（2）當(dāng)a≠0時，若f（x）是減函數(shù)，求a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
.
(1)當(dāng)
時，求證： 
；
(2)設(shè)函數(shù)
，且
有兩個不同的零點
，
①求實數(shù)
的取值范圍； ②求證： 
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知集合A={x|y= 
}，B={x|log2x≤1}，則A∩B=（ ）
A.{x|﹣3≤x≤1}
B.{x|0＜x≤1}
C.{x|﹣3≤x≤2}
D.{x|x≤2}
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】若x，y滿足約束條件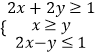 
，且向量 
=（3，2）， 
=（x，y），則 的取值范圍（ ）
A.[ 
，5]
B.[ 
，5]
C.[ ，4]
D.[ ，4]
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在四棱錐
中，四邊形
是菱形， 
，平面
平面
在棱
上運動.
（1）當(dāng)
在何處時， 
平面
；
（2）已知
為
的中點， 
與
交于點
，當(dāng)
平面
時，求三棱錐
的體積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
