
【題目】已知函數f(x)=2cos2x+2 ![]() sinxcosx+a,且當
sinxcosx+a,且當 ![]() 時,f(x)的最小值為2.
時,f(x)的最小值為2.
(1)求a的值,并求f(x)的單調增區間;
(2)將函數y=f(x)的圖象上各點的縱坐標保持不變,橫坐標縮短到原來的 ![]() ,再把所得圖象向右平移
,再把所得圖象向右平移 ![]() 個單位,得到函數y=g(x),求方程g(x)=2在區間
個單位,得到函數y=g(x),求方程g(x)=2在區間 ![]() 上的所有根之和.
上的所有根之和.
【答案】
(1)解:f(x)=2cos2x+2 ![]() sinxcosx+a
sinxcosx+a
=cos2x+1+ ![]() sin2x+a
sin2x+a
=2sin(2x+ ![]() )+a+1,
)+a+1,
∵x∈[0, ![]() ],
],
∴2x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
∴f(x)min=a+2=2,故a=0,
∴f(x)=2sin(2x+ ![]() )+1,
)+1,
由2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() (k∈Z),
(k∈Z),
解得:kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() (k∈Z),
(k∈Z),
故f(x)的單調增區間是[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
(2)解:g(x)=2sin[4(x﹣ ![]() )+
)+ ![]() ]+1=2sin(4x﹣
]+1=2sin(4x﹣ ![]() )+1,
)+1,
由g(x)=2得sin(4x﹣ ![]() )=
)= ![]() ,
,
則4x﹣ ![]() =2kπ+
=2kπ+ ![]() 或2kπ+
或2kπ+ ![]() (k∈Z),
(k∈Z),
解得x= ![]() +
+ ![]() 或
或 ![]() +
+ ![]() ,(k∈Z);
,(k∈Z);
∵x∈[0, ![]() ],
],
∴x= ![]() 或
或 ![]() ,故方程所有根之和為
,故方程所有根之和為 ![]() +
+ ![]() =
= ![]()
【解析】(1)利用三角函數中的恒等變換應用,可求得f(x)=2sin(2x+ ![]() )+a+1,x∈[0,
)+a+1,x∈[0, ![]() ]時f(x)的最小值為2,可求得a,利用正弦函數的單調性可求f(x)的單調增區間;(2)利用函數y=Asin(ωx+φ)的圖象變換,可求得g(x)=2sin(4x﹣
]時f(x)的最小值為2,可求得a,利用正弦函數的單調性可求f(x)的單調增區間;(2)利用函數y=Asin(ωx+φ)的圖象變換,可求得g(x)=2sin(4x﹣ ![]() )+1,依題意,g(x)=2得sin(4x﹣
)+1,依題意,g(x)=2得sin(4x﹣ ![]() )=
)= ![]() ,x∈[0,
,x∈[0, ![]() ],可求得x=
],可求得x= ![]() 或
或 ![]() ,從而可得答案.
,從而可得答案.
【考點精析】利用函數y=Asin(ωx+φ)的圖象變換對題目進行判斷即可得到答案,需要熟知圖象上所有點向左(右)平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的橫坐標伸長(縮短)到原來的
的圖象上所有點的橫坐標伸長(縮短)到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的縱坐標伸長(縮短)到原來的
的圖象上所有點的縱坐標伸長(縮短)到原來的![]() 倍(橫坐標不變),得到函數
倍(橫坐標不變),得到函數![]() 的圖象.
的圖象.


科目:高中數學 來源: 題型:
【題目】已知 ![]() ,則導函數f′(x)是( )
,則導函數f′(x)是( )
A.僅有最小值的奇函數
B.既有最大值,又有最小值的偶函數
C.僅有最大值的偶函數
D.既有最大值,又有最小值的奇函數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在△ABC中,AD⊥BC于D,下列條件:
①∠B+∠DAC=90°,
②∠B=∠DAC,
③![]() ,
,
④AB2=BD·BC.
其中一定能夠判定△ABC是直角三角形的共有( )
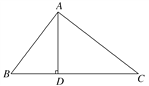
A. 3個 B. 2個 C. 1個 D. 0個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知y=f(x)是奇函數,當x∈(0,2)時,f(x)=lnx﹣ax(a> ![]() ),當x∈(﹣2,0)時,f(x)的最小值為1,則a的值等于 .
),當x∈(﹣2,0)時,f(x)的最小值為1,則a的值等于 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的頂點在原點,焦點在
的頂點在原點,焦點在![]() 軸上,且拋物線上有一點
軸上,且拋物線上有一點![]() 到焦點的距離為5.
到焦點的距離為5.
(1)求該拋物線![]() 的方程;
的方程;
(2)已知拋物線上一點![]() ,過點
,過點![]() 作拋物線的兩條弦
作拋物線的兩條弦![]() 和
和![]() ,且
,且![]() ,判斷直線
,判斷直線![]() 是否過定點?并說明理由.
是否過定點?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】把函數y=sin(x﹣ ![]() )的圖象向左平移
)的圖象向左平移 ![]() 個單位長度,再將圖象上所有點的橫坐標縮短為原來的
個單位長度,再將圖象上所有點的橫坐標縮短為原來的 ![]() 倍(縱坐標不變)得到函數f(x)的圖象. (Ⅰ)寫出函數f(x)的解析式;
倍(縱坐標不變)得到函數f(x)的圖象. (Ⅰ)寫出函數f(x)的解析式;
(Ⅱ)若x∈[0, ![]() ]時,關于x的方程f(x)﹣m=0有兩個不等的實數根,求實數m的取值范圍.
]時,關于x的方程f(x)﹣m=0有兩個不等的實數根,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com