
【題目】為了在夏季降溫和冬季取暖時減少能源消耗,業主決定對房屋的屋頂和外墻噴涂某種新型隔熱材料,該材料有效使用年限為20年.已知房屋外表噴一層這種隔熱材料的費用為每毫米厚6萬元,且每年的能源消耗費用![]() (萬元)與隔熱層厚度
(萬元)與隔熱層厚度![]() (毫米)滿足關系:
(毫米)滿足關系:![]() .設
.設![]() 為隔熱層建造費用與
為隔熱層建造費用與![]() 年的能源消耗費用之和.
年的能源消耗費用之和.
(1)請解釋![]() 的實際意義,并求
的實際意義,并求![]() 的表達式;
的表達式;
(2)當隔熱層噴涂厚度為多少毫米時,業主所付的總費用![]() 最少?并求此時與不建隔熱層相比較,業主可節省多少錢?
最少?并求此時與不建隔熱層相比較,業主可節省多少錢?
科目:高中數學 來源: 題型:
【題目】設全集為R,函數 ![]() 的定義域為M,則RM為( )
的定義域為M,則RM為( )
A.[﹣1,1]
B.(﹣1,1)
C.(﹣∞,﹣1]∪[1,+∞)
D.(﹣∞,﹣1)∪(1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠家擬在2019年舉行促銷活動,經過調查測算,該產品的年銷量(即該廠的年產量)![]() (單位:萬件)與年促銷費用
(單位:萬件)與年促銷費用![]() (
(![]() )(單位:萬元)滿足
)(單位:萬元)滿足![]() (
(![]() 為常數),如果不搞促銷活動,則該產品的年銷量只能是1萬件. 已知2019年生產該產品的固定投入為6萬元,每生產1萬件該產品需要再投入12萬元,廠家將每件產品的銷售價格定為每件產品平均成本的1.5倍(產品成本包括固定投入和再投入兩部分).
為常數),如果不搞促銷活動,則該產品的年銷量只能是1萬件. 已知2019年生產該產品的固定投入為6萬元,每生產1萬件該產品需要再投入12萬元,廠家將每件產品的銷售價格定為每件產品平均成本的1.5倍(產品成本包括固定投入和再投入兩部分).
(1)將該廠家2019年該產品的利潤![]() 萬元表示為年促銷費用
萬元表示為年促銷費用![]() 萬元的函數;
萬元的函數;
(2)該廠家2019年的年促銷費用投入多少萬元時,廠家利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)已知過原點的動直線![]() 與圓
與圓![]()
![]() 相交于不同的兩點
相交于不同的兩點![]() ,
,![]() .
.
(1)求圓![]() 的圓心坐標;
的圓心坐標;
(2)求線段![]() 的中點
的中點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(3)是否存在實數![]() ,使得直線
,使得直線![]()
![]() 與曲線
與曲線![]() 只有一個交點?若存在,求出
只有一個交點?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD-A1B1C1D1中,E,F分別是C1D1,CC1的中點,則異面直線AE與BF所成角的余弦值為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓C: ![]() 經過點P(1,
經過點P(1, ![]() ),離心率e=
),離心率e= ![]() ,直線l的方程為x=4.
,直線l的方程為x=4. 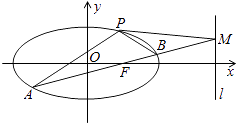
(1)求橢圓C的方程;
(2)AB是經過右焦點F的任一弦(不經過點P),設直線AB與直線l相交于點M,記PA,PB,PM的斜率分別為k1 , k2 , k3 . 問:是否存在常數λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com