
設(shè)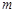 是給定的正整數(shù),有序數(shù)組(
是給定的正整數(shù),有序數(shù)組(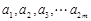 )中
)中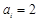 或
或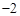
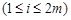 .
.
(1)求滿足“對(duì)任意的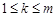 ,
,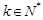 ,都有
,都有 ”的有序數(shù)組(
”的有序數(shù)組(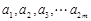 )的個(gè)數(shù)
)的個(gè)數(shù) ;
;
(2)若對(duì)任意的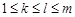 ,
,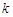 ,
, ,都有
,都有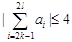 成立,求滿足“存在
成立,求滿足“存在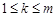 ,使得
,使得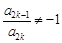 ”的有序數(shù)組(
”的有序數(shù)組(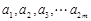 )的個(gè)數(shù)
)的個(gè)數(shù) .
.
(1)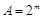 ,(2)
,(2)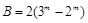 .
.
解析試題分析:
(1)正確理解每一偶數(shù)項(xiàng)與前相鄰奇數(shù)項(xiàng)是相反數(shù),而與后相鄰奇數(shù)項(xiàng)相等或相反;因此分組按(奇、偶)分為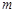 組,每組有2種可能,各組可能互不影響,共有
組,每組有2種可能,各組可能互不影響,共有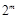 種可能,
種可能,
(2)在(1)的基礎(chǔ)上,某些組可能為(2,2)或(-2,-2),需討論這些組個(gè)數(shù)的情況,最少一個(gè),最多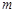 個(gè).另外條件“對(duì)任意的
個(gè).另外條件“對(duì)任意的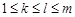 ,
,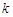 ,
, ,都有
,都有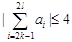 成立”控制不能出現(xiàn)各組都為2或-2的情況,而是間隔出現(xiàn)(2,2)、(-2,-2).
成立”控制不能出現(xiàn)各組都為2或-2的情況,而是間隔出現(xiàn)(2,2)、(-2,-2).
試題解析:
解:(1)因?yàn)閷?duì)任意的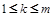 ,都有
,都有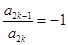 ,則
,則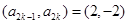 或
或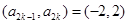
共有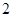 種,所以
種,所以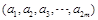 共有
共有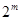 種不同的選擇,所以
種不同的選擇,所以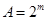 . 5分
. 5分
(2)當(dāng)存在一個(gè)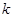 時(shí),那么這一組有
時(shí),那么這一組有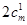 種,其余的由(1)知有
種,其余的由(1)知有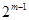 ,所有共有
,所有共有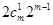 ;
;
當(dāng)存在二個(gè)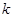 時(shí),因?yàn)闂l件對(duì)任意的
時(shí),因?yàn)闂l件對(duì)任意的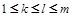 ,都有
,都有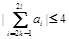 成立得這兩組共有
成立得這兩組共有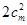 ,
,
其余的由(1)知有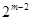 ,所有共有
,所有共有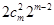 ;
;
依次類推得: . 10分
. 10分
考點(diǎn):分步(乘法)計(jì)數(shù)原理,二項(xiàng)式定理應(yīng)用.


 新思維假期作業(yè)寒假吉林大學(xué)出版社系列答案
新思維假期作業(yè)寒假吉林大學(xué)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知 的展開式的二項(xiàng)式系數(shù)的和比(3x-1)n的展開式的二項(xiàng)式系數(shù)和大992,求(2x-
的展開式的二項(xiàng)式系數(shù)的和比(3x-1)n的展開式的二項(xiàng)式系數(shù)和大992,求(2x-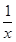 )2n的展開式中,(1)二項(xiàng)式系數(shù)最大的項(xiàng);(2)系數(shù)的絕對(duì)值最大的項(xiàng).
)2n的展開式中,(1)二項(xiàng)式系數(shù)最大的項(xiàng);(2)系數(shù)的絕對(duì)值最大的項(xiàng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某醫(yī)院有內(nèi)科醫(yī)生12名,外科醫(yī)生8名,現(xiàn)選派5名參加賑災(zāi)醫(yī)療隊(duì),其中
(1)某內(nèi)科醫(yī)生甲與某外科醫(yī)生乙必須參加,共有多少種不同選法?
(2)甲、乙均不能參加,有多少種選法?
(3)甲、乙兩人至少有一人參加,有多少種選法?
(4)隊(duì)中至少有一名內(nèi)科醫(yī)生和一名外科醫(yī)生,有幾種選法?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知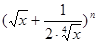 的展開式前三項(xiàng)中的
的展開式前三項(xiàng)中的 的系數(shù)成等差數(shù)列.
的系數(shù)成等差數(shù)列.
(1)求展開式中所有的 的有理項(xiàng);(2)求展開式中系數(shù)最大的項(xiàng).
的有理項(xiàng);(2)求展開式中系數(shù)最大的項(xiàng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
已知二項(xiàng)式 (
(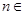 N*)展開式中,前三項(xiàng)的二項(xiàng)式系數(shù)和是
N*)展開式中,前三項(xiàng)的二項(xiàng)式系數(shù)和是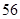 ,求:
,求:
(Ⅰ)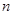 的值;
的值;
(Ⅱ)展開式中的常數(shù)項(xiàng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知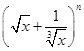 的展開式的二項(xiàng)式系數(shù)之和比(a+b)2n的展開式的系數(shù)之和小240,求
的展開式的二項(xiàng)式系數(shù)之和比(a+b)2n的展開式的系數(shù)之和小240,求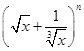 n的展開式中系數(shù)最大的項(xiàng).
n的展開式中系數(shù)最大的項(xiàng).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com