Question

【題目】如圖，在多面體中，底面為正方形，四邊形是矩形，平面平面.

（1）求證：平面平面；

（2）若過直線的一個平面與線段和分別相交于點和 (點與點均不重合），求證： ；

（3）判斷線段上是否存在一點，使得平面平面?若存在，求的值；若不存在，請說明理由.

Answer 1

【答案】（1）見解析（2）見解析（3）

【解析】試題分析：（1）要證面面垂直，先找線面垂直，證平面，最終得到面面垂直；（2）根據線面平行的性質定理得到平面，再由線面平行的判定定理得到結論；（3）取CE的中點M，證兩個平面的兩條相交直線互相平行，得到面面平行，進而得到比值。

解析：

（Ⅰ）因為四邊形是正方形，

所以.

又因為平面平面，平面平面，

且平面，

所以平面.

又因為平面，

所以平面平面.

（Ⅱ）由題意， ， 平面， 平面，

所以平面，

又因為平面，平面平面，

所以.

（Ⅲ）線段上存在一點，使得平面平面，此時.

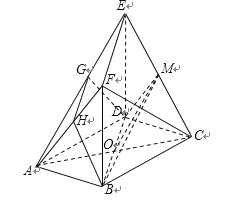
以下給出證明過程.

設的中點為，連接， ，

因為， 平面， 平面，

所以平面.

設，連接，

在中，因為， ，

所以，

又因為平面， 平面，

所以平面.又因為， 平面，

所以平面平面.