【題目】已知函數f（x）=x2+（m+2）x+（2m+5）（m≠0）的兩個零點分別在區間（﹣1，0）和區間（1，2）內，則實數m的取值范圍是 ．
【答案】﹣ 
＜m＜﹣ 
【解析】解：由f（x）=x2+（m+2）x+（2m+5）（m≠0）的圖像開口向上，兩個零點分別在區間（﹣1，0）和區間（1，2）內，則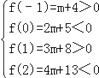 
解不等式可得﹣ ＜m＜﹣
所以答案是：﹣ ＜m＜﹣ ．
【考點精析】利用二次函數的性質和函數的零點與方程根的關系對題目進行判斷即可得到答案，需要熟知當
時，拋物線開口向上，函數在
上遞減，在
上遞增；當
時，拋物線開口向下，函數在上遞增，在上遞減；二次函數的零點：（1）△＞0，方程 有兩不等實根，二次函數的圖象與 軸有兩個交點，二次函數有兩個零點;（2）△＝0，方程 有兩相等實根（二重根），二次函數的圖象與 軸有一個交點，二次函數有一個二重零點或二階零點;（3）△＜0，方程 無實根，二次函數的圖象與 軸無交點，二次函數無零點．
科目：高中數學 來源： 題型：
【題目】有三個游戲規則如表，袋子中分別裝有形狀、大小相同的球，從袋中無放回地取球，
游戲1 | 游戲2 | 游戲3 |
袋中裝有3個黑球和2個白球 | 袋中裝有2個黑球和2個白球 | 袋中裝有3個黑球和1個白球 |
從袋中取出2個球 | 從袋中取出2個球 | 從袋中取出2個球 |
若取出的兩個球同色，則甲勝 | 若取出的兩個球同色，則甲勝 | 若取出的兩個球同色，則甲勝 |
若取出的兩個球不同色，則乙勝 | 若取出的兩個球不同色，則乙勝 | 若取出的兩個球不同色，則乙勝 |
問其中不公平的游戲是（ ）
A.游戲2
B.游戲3
C.游戲1和游戲2
D.游戲1和游戲3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義域為R的奇函數f（x）= 
，其中h（x）是指數函數，且h（2）=4．
（1）求函數f（x）的解析式；
（2）求不等式f（2x﹣1）＞f（x+1）的解集．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解某社區居民的家庭年收入與年支出的關系，相關部門隨機調查了該社區5戶家庭，得到如表統計數據表：
收入x（萬元） | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y（萬元） | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
（1）根據上表可得回歸直線方程 
= 
x+ 
，其中 =0.76， = 
﹣ 
，據此估計，該社區一戶年收入為15萬元的家庭年支出為多少？
（2）若從這5個家庭中隨機抽選2個家庭進行訪談，求抽到家庭的年收入恰好一個不超過10萬元，另一個超過11萬元的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】張先生知道清晨從甲地到乙地有好、中、差三個班次的客車．但不知道具體誰先誰后．他打算：第一輛看后一定不坐，若第二輛比第一輛舒服，則乘第二輛；否則坐第三輛．問張先生坐到好車的概率和坐到差車的概率分別是（ ）
A.
、
B.
、
C. 、 
D.
、
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量 
=（sinθ，﹣2）與 
=（1，cosθ）互相垂直，其中θ∈（0， 
）．
（Ⅰ）求sinθ和cosθ的值；
（Ⅱ）若sin（θ﹣φ）= 
，0＜φ＜ ，求cosφ的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
，g（x）=f（x）﹣a
（1）當a=2時，求函數g（x）的零點；
（2）若函數g（x）有四個零點，求a的取值范圍；
（3）在（2）的條件下，記g（x）得四個零點分別為x1 ， x2 ， x3 ， x4 ， 求x1+x2+x3+x4的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量 
=（cos 
，sin ）， 
=（cos 
，﹣sin ），且x∈[ 
，π]．
（1）求 及| + |；
（2）求函數f（x）= +| + |的最大值，并求使函數取得最大值時x的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】袋中有質地、大小完全相同的5個小球，編號分別為1，2，3，4，5，甲、乙兩人玩一種游戲．甲先摸出一個球．記下編號，放回后再摸出一個球，記下編號，如果兩個編號之和為偶數．則算甲贏，否則算乙贏．
（1）求甲贏且編號之和為6的事件發生的概率：
（2）試問：這種游戲規則公平嗎．請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com