【題目】張先生知道清晨從甲地到乙地有好、中、差三個班次的客車．但不知道具體誰先誰后．他打算：第一輛看后一定不坐，若第二輛比第一輛舒服，則乘第二輛；否則坐第三輛．問張先生坐到好車的概率和坐到差車的概率分別是（ ）
A.
、
B.
、
C. 、 
D.
、
【答案】C
【解析】解：設三輛車的等次為：下 中 上，它們的先后次序分下列6種情況， 下 中 上 他乘上中等車
下 上 中 他乘上上等車
中 下 上 他乘上上等車
中 上 下 他乘上上等車
上 下 中 他乘上中等車
上 中 下 他乘上下等車
他乘上上等車的情況數為：3
那么他乘上上等車的概率為 
他乘上下等車的情況數為：1
那么他乘上下等車的概率為 
．
故選C．
本題考查的知識點是古典概型，設三輛車的等次為：下 中 上，我們分6種情況，下 中 上 他沒乘上上等車；下 上 中 他乘上上等車；中 下 上 他乘上上等車；中 上 下 他乘上上等車；上 下 中 他沒乘上上等車；上 中 下 他沒乘上上等車；一共6種情形，然后代入古典概型公式計算，即可得到答案．
科目：高中數學 來源： 題型：
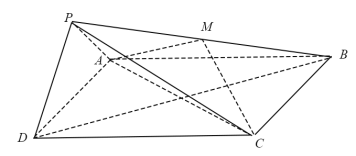
【題目】如圖，在四棱錐P-ABCD中，底面ABCD為正方形，平面PAD⊥平面ABCD，點M在線段PB上，PD//平面MAC，PA=PD=
，AB=4．
（I）求證：M為PB的中點；
（II）求二面角B-PD-A的大小；
（III）求直線MC與平面BDP所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x2+2bx+c，且f（1）=f（3）=﹣1．設a＞0，將函數f（x）的圖像先向右平移a個單位長度，再向下平移a2個單位長度，得到函數g（x）的圖像． （Ⅰ）若函數g（x）有兩個零點x1 ， x2 ， 且x1＜4＜x2 ， 求實數a的取值范圍；
（Ⅱ）設連續函數在區間[m，n]上的值域為[λ，μ]，若有 
，則稱該函數為“陡峭函數”．若函數g（x）在區間[a，2a]上為“陡峭函數”，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知四棱錐P﹣ABCD中，底面ABCD是棱長為2的菱形，PA⊥平面ABCD，∠ABC=60°，E是BC中點，若H為PD上的動點，EH與平面PAD所成最大角的正切值為 
． 
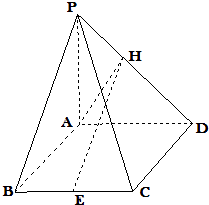
（1）當EH與平面PAD所成角的正切值為 時，求證：EH∥平面PAB；
（2）在（1）的條件下，求二面角A﹣PB﹣C的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高一（2）班共有60名同學參加期末考試，現將其數學學科成績（均為整數）分成六個分數段[40，50），[50，60），…，[90，100]，畫出如如圖所示的部分頻率分布直方圖，請觀察圖形信息，回答下列問題：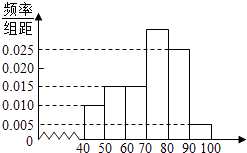 
（1）求70～80分數段的學生人數；
（2）估計這次考試中該學科的優分率（80分及以上為優分）、中位數、平均值；
（3）現根據本次考試分數分成下列六段（從低分段到高分段依次為第一組、第二組、…、第六組）為提高本班數學整體成績，決定組與組之間進行幫扶學習．若選出的兩組分數之差大于30分（以分數段為依據，不以具體學生分數為依據），則稱這兩組為“最佳組合”，試求選出的兩組為“最佳組合”的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
， 
， 
．
（1）討論函數
的單調性；
（2）記
，設
， 
為函數
圖象上的兩點，且
．
（ⅰ）當
， 
時，若
在
處的切線相互垂直，求證： 
；
（ⅱ）若
在點
處的切線重合，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，橢圓
的左、右焦點分別為F1，F2，離心率為
，兩準線之間的距離為8.點P在橢圓E上，且位于第一象限，過點F1作直線PF1的垂線l1,過點F2作直線PF2的垂線l2.
（1）求橢圓E的標準方程；
（2）若直線l1，l2的交點Q在橢圓E上，求點P的坐標.
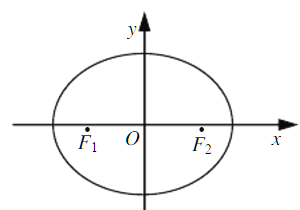
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
