
【題目】在![]() 中,
中, ![]() 所對(duì)的邊分別為
所對(duì)的邊分別為![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點(diǎn),求
的中點(diǎn),求![]() 的長(zhǎng).
的長(zhǎng).
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)由已知,利用正弦定理可得![]() a2=
a2=![]() b2+
b2+![]() c2-2b,再利用余弦定理即可得出cosA,結(jié)合A的范圍即可得解A的值.
c2-2b,再利用余弦定理即可得出cosA,結(jié)合A的范圍即可得解A的值.
(2)△ABC中,先由正弦定理求得AC的值,再由余弦定理求得AB的值,△ABD中,由余弦定理求得BD的值.
試題解析:
(1)因?yàn)?/span>![]() asin A=(
asin A=(![]() b-c)sin B+(
b-c)sin B+(![]() c-b)·sin C,
c-b)·sin C,
由正弦定理得![]() a2=(
a2=(![]() b-c)b+(
b-c)b+(![]() c-b)c,
c-b)c,
整理得![]() a2=
a2=![]() b2+
b2+![]() c2-2bc,
c2-2bc,
由余弦定理得cos A=![]() =
=![]() =
=![]() ,
,
因?yàn)?/span>A∈(0,π),所以A=![]() .
.
(2)由cos B=![]() ,得sin B=
,得sin B=![]() =
=![]() =
=![]() ,
,
所以cos C=cos[π-(A+B)]=-cos(A+B)=-![]() =-
=-![]() ,
,
由正弦定理得b=![]() =
=![]() =2,
=2,
所以CD=![]() AC=1,
AC=1,
在△BCD中,由余弦定理得BD2=(![]() )2+12-2×1×
)2+12-2×1×![]() ×
×![]() =13,
=13,
所以BD=![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)數(shù)列{an}的前n項(xiàng)和是Sn , 若點(diǎn)An(n, ![]() )在函數(shù)f(x)=﹣x+c的圖象上運(yùn)動(dòng),其中c是與x無(wú)關(guān)的常數(shù),且a1=3(n∈N*).
)在函數(shù)f(x)=﹣x+c的圖象上運(yùn)動(dòng),其中c是與x無(wú)關(guān)的常數(shù),且a1=3(n∈N*).
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)記bn=a ![]() ,求數(shù)列{bn}的前n項(xiàng)和Tn的最小值.
,求數(shù)列{bn}的前n項(xiàng)和Tn的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某投資人欲將5百萬(wàn)元獎(jiǎng)金投入甲、乙兩種理財(cái)產(chǎn)品,根據(jù)銀行預(yù)測(cè),甲、乙兩種理財(cái)產(chǎn)品的收益與投入獎(jiǎng)金![]() 的關(guān)系式分別為
的關(guān)系式分別為![]() ,其中
,其中![]() 為常數(shù)且
為常數(shù)且![]() .設(shè)對(duì)乙種產(chǎn)品投入獎(jiǎng)金
.設(shè)對(duì)乙種產(chǎn)品投入獎(jiǎng)金![]() 百萬(wàn)元,其中
百萬(wàn)元,其中![]() .
.
(1)當(dāng)![]() 時(shí),如何進(jìn)行投資才能使得總收益
時(shí),如何進(jìn)行投資才能使得總收益![]() 最大;(總收益
最大;(總收益![]() )
)
(2)銀行為了吸儲(chǔ),考慮到投資人的收益,無(wú)論投資人獎(jiǎng)金如何分配,要使得總收益不低于![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】公差不為0的等差數(shù)列![]() 中,已知
中,已知![]() 且
且![]() ,其前
,其前![]() 項(xiàng)和
項(xiàng)和![]() 的最大值為( )
的最大值為( )
A. 25 B. 26 C. 27 D. 28
【答案】B
【解析】設(shè)等差數(shù)列![]() 的公差為
的公差為![]() ,
,
∵![]() ,
,
∴![]() ,
,
整理得![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴當(dāng)![]() 時(shí),
時(shí), ![]() .
.
故![]() 最大,且
最大,且![]() .選B.
.選B.
點(diǎn)睛:求等差數(shù)列前n項(xiàng)和最值的常用方法:
①利用等差數(shù)列的單調(diào)性, 求出其正負(fù)轉(zhuǎn)折項(xiàng),便可求得和的最值;
②將等差數(shù)列的前n項(xiàng)和![]() (A、B為常數(shù))看作關(guān)于n的二次函數(shù),根據(jù)二次函數(shù)的性質(zhì)求最值.
(A、B為常數(shù))看作關(guān)于n的二次函數(shù),根據(jù)二次函數(shù)的性質(zhì)求最值.
【題型】單選題
【結(jié)束】
9
【題目】如圖,網(wǎng)格紙上小正方形的邊長(zhǎng)為1,粗實(shí)線畫出的是某多面體的三視圖,則該多面體的表面積為( )
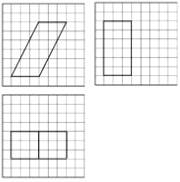
A. ![]() B.
B. ![]() C. 90 D. 81
C. 90 D. 81
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某網(wǎng)店統(tǒng)計(jì)了連續(xù)三天售出商品的種類情況:第一天售出19種商品,第二天售出13種商品,第三天售出18種商品;前兩天都售出的商品有3種,后兩天都售出的商品有4種,則該網(wǎng)店
①第一天售出但第二天未售出的商品有______種;
②這三天售出的商品最少有_______種.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 滿足
滿足![]() ,若函數(shù)
,若函數(shù)![]() 與
與![]() 圖象的交點(diǎn)為
圖象的交點(diǎn)為![]() ,則交點(diǎn)的所有橫坐標(biāo)和縱坐標(biāo)之和為( )
,則交點(diǎn)的所有橫坐標(biāo)和縱坐標(biāo)之和為( )
A. 0 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四棱錐P﹣ABCD的底面ABCD是正方形,側(cè)棱PD⊥底面ABCD,PD=DC,E是PC的中點(diǎn). 
(1)證明PA∥平面BDE;
(2)證明:DE⊥面PBC;
(3)求直線AB與平面PBC所成角的大小.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com