
【題目】已知函數![]() ,在點
,在點![]() 處的切線方程為
處的切線方程為![]() ,求(1)實數
,求(1)實數![]() 的值;(2)函數
的值;(2)函數![]() 的單調區間以及在區間
的單調區間以及在區間![]() 上的最值.
上的最值.
【答案】(1)![]() (2)
(2)![]()
【解析】試題分析:(1)由題已知點![]() 處的切線方程
處的切線方程![]() ,可獲得兩個條件;即:點
,可獲得兩個條件;即:點![]()
再函數的圖像上,令點![]() 處的導數為切線斜率。可得兩個方程,求出
處的導數為切線斜率。可得兩個方程,求出![]() 的值
的值
(2)由(1)已知函數的解析式,可運用導數求出函數的單調區間和最值。即:
![]() 為函數的增區間,反之為減區間。最值需求出極值與區間端點值比較而得。
為函數的增區間,反之為減區間。最值需求出極值與區間端點值比較而得。
試題解析:(1)因為在點![]() 處的切線方程為
處的切線方程為![]() ,所以切線斜率是
,所以切線斜率是![]() ,
,
且![]() ,求得
,求得![]() ,即點
,即點![]() ,
,
又函數![]() ,則
,則![]()
所以依題意得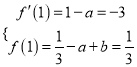 ,解得
,解得![]()
(2)由(1)知![]() ,所以
,所以![]()
令![]() ,解得
,解得![]() ,當
,當![]() ;當
;當![]()
所以函數![]() 的單調遞增區間是
的單調遞增區間是![]() ,單調遞減區間是
,單調遞減區間是![]()
又![]() ,所以當x變化時,f(x)和f′(x)變化情況如下表:
,所以當x變化時,f(x)和f′(x)變化情況如下表:
X | 0 | (0,2) | 2 | (2,3) | 3 |
f′(x) | - | 0 | + | 0 | |
f(x) | 4 | ↘ | 極小值 | ↗ | 1 |
所以當![]() 時,
時, ![]() ,
, ![]()


科目:高中數學 來源: 題型:
【題目】給出下列五個命題:
①函數f(x)=2a2x-1-1的圖象過定點(![]() ,-1);
,-1);
②已知函數f(x)是定義在R上的奇函數,當x≥0時,f(x)=x(x+1),若f(a)=-2則實數a=-1或2.
③若loga![]() >1,則a的取值范圍是(
>1,則a的取值范圍是(![]() ,1);
,1);
④若對于任意x∈R都f(x)=f(4-x)成立,則f(x)圖象關于直線x=2對稱;
⑤對于函數f(x)=lnx,其定義域內任意x1≠x2都滿足f(![]() )≥
)≥![]()
其中所有正確命題的序號是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)在復數范圍內解方程![]() (
(![]() 為虛數單位)
為虛數單位)
(2)設![]() 是虛數,
是虛數,![]() 是實數,且
是實數,且![]()
(i)求![]() 的值及
的值及![]() 的實部的取值范圍;
的實部的取值范圍;
(ii)設![]() ,求證:
,求證:![]() 為純虛數;
為純虛數;
(iii)在(ii)的條件下求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中錯誤的個數是( )
①若直線![]() 平面
平面![]() ,直線
,直線![]() ,則
,則![]() ;②若直線l和平面
;②若直線l和平面![]() 內的無數條直線垂直,則直線l與平面
內的無數條直線垂直,則直線l與平面![]() 必相交;③過平面
必相交;③過平面![]() 外一點有且只有一條直線和平面
外一點有且只有一條直線和平面![]() 垂直;④過直線
垂直;④過直線![]() 外一點有且只有一個平面和直線a垂直
外一點有且只有一個平面和直線a垂直
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年2月22日.在平昌冬奧會短道速滑男子500米比賽中.中國選手武大靖以連續打破世界紀錄的優異表現,為中國代表隊奪得了本屆冬奧會的首枚金牌,也創造中國男子冰上競速項目在冬奧會金牌零的突破.某高校為調查該校學生在冬奧會期間累計觀看冬奧會的時間情況.收集了200位男生、100位女生累計觀看冬奧會時間的樣本數據(單位:小時).又在100位女生中隨機抽取20個人.已知這20位女生的數據莖葉圖如圖所示.
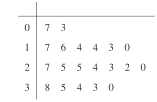
(1)將這20位女生的時間數據分成8組,分組區間分別為![]() ,在答題卡上完成頻率分布直方圖;
,在答題卡上完成頻率分布直方圖;
(2)以(1)中的頻率作為概率,求1名女生觀看冬奧會時間不少于30小時的概率;
(3)以(1)中的頻率估計100位女生中累計觀看時間小于20個小時的人數.已知200位男生中累計觀看時間小于20小時的男生有50人請完成答題卡中的列聯表,并判斷是否有99 %的把握認為“該校學生觀看冬奧會累計時間與性別有關”.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
附:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的定義域;
的定義域;
(2)若函數![]() 有且僅有一個零點,求實數m的取值范圍;
有且僅有一個零點,求實數m的取值范圍;
(3)任取![]() ,若不等式
,若不等式![]() 對任意
對任意![]() 恒成立,求實數m的取值范圍.
恒成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com