
【題目】如圖,在三棱錐中,SA=SB=AB=BC=CA=6,且側面ASB⊥底面ABC,則三棱錐S-ABC外接球的表面積為( )

A. 60π B. 56π C. 52π D. 48π
科目:高中數學 來源: 題型:
【題目】如圖,已知點P是平行四邊形ABCD所在平面外一點,M、N分別是AB、PC的中點.

(1)求證:MN∥平面PAD;
(2)在PB上確定一個點Q,使平面MNQ∥平面PAD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義域為R的函數f(x)在(2,+∞)上單調遞減,且y=f(x+2)為偶函數,則關于x的不等式f(2x﹣1)﹣f(x+1)>0的解集為( )
A.(﹣∞,﹣ ![]() )∪(2,+∞)
)∪(2,+∞)
B.(﹣ ![]() ,2)
,2)
C.(﹣∞, ![]() )∪(2,+∞)
)∪(2,+∞)
D.( ![]() ,2)
,2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的圓心在坐標原點,且與直線
的圓心在坐標原點,且與直線![]() 相切.
相切.
(1)求直線![]() 被圓
被圓![]() 所截得的弦
所截得的弦![]() 的長;
的長;
(2)過點![]() 作兩條與圓
作兩條與圓![]() 相切的直線,切點分別為
相切的直線,切點分別為![]() 求直線
求直線![]() 的方程;
的方程;
(3)若與直線![]() 垂直的直線
垂直的直線![]() 與圓
與圓![]() 交于不同的兩點
交于不同的兩點![]() ,若
,若![]() 為鈍角,求直線
為鈍角,求直線![]() 在
在![]() 軸上的截距的取值范圍.
軸上的截距的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C1的參數方程是 ![]() (φ為參數),以坐標原點為極點,x軸的非負半軸為極軸建立極坐標系,曲線C2的極坐標系方程是
(φ為參數),以坐標原點為極點,x軸的非負半軸為極軸建立極坐標系,曲線C2的極坐標系方程是 ![]() ,正方形ABCD的頂點都在C1上,且A,B,C,D依逆時針次序排列,點A的極坐標為
,正方形ABCD的頂點都在C1上,且A,B,C,D依逆時針次序排列,點A的極坐標為 ![]() .
.
(1)求點A,B,C,D的直角坐標;
(2)設P為C2上任意一點,求|PA|2+|PB|2+|PC|2+|PD|2的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐P﹣ABCD中,直線AP,AB,AD兩兩相互垂直,且AD∥BC,AP=AB=AD=2BC. 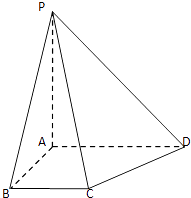
(1)求異面直線PC與BD所成角的余弦值;
(2)求鈍二面角B﹣PC﹣D的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,其中
,其中![]() .已知
.已知![]() .
.
(Ⅰ)求![]() .
.
(Ⅱ)將函數![]() 的圖象上各點的橫坐標伸長為原來的
的圖象上各點的橫坐標伸長為原來的![]() 倍(縱坐標不變),再將得到的圖象向左平移
倍(縱坐標不變),再將得到的圖象向左平移![]() 個單位,得到函數
個單位,得到函數![]() 的圖象,求
的圖象,求![]() 在
在![]() 上的最小值.
上的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com