
如圖,在直角坐標(biāo)系xOy中,已知橢圓![]() 的離心率e=
的離心率e=![]() ,左右兩個(gè)焦分別為F1、F2.過右焦點(diǎn)F2且與x軸垂直的直線與橢圓C相交M、N兩點(diǎn),且|MN|=1.
,左右兩個(gè)焦分別為F1、F2.過右焦點(diǎn)F2且與x軸垂直的直線與橢圓C相交M、N兩點(diǎn),且|MN|=1.

(Ⅰ)求橢圓C的方程;
(Ⅱ)設(shè)橢圓C的左頂點(diǎn)為A,下頂點(diǎn)為B,動(dòng)點(diǎn)P滿足![]() ,(
,(![]() )試求點(diǎn)P的軌跡方程,使點(diǎn)B關(guān)于該軌跡的對稱點(diǎn)落在橢圓C上.
)試求點(diǎn)P的軌跡方程,使點(diǎn)B關(guān)于該軌跡的對稱點(diǎn)落在橢圓C上.
解:(Ⅰ)∵![]() 軸,∴
軸,∴![]() ,由橢圓的定義得:
,由橢圓的定義得:![]() , 2分
, 2分
∵![]() ,∴
,∴![]() , 4分
, 4分
又![]() 得
得![]() ∴
∴![]()
![]()
![]()
∴![]() , 6分
, 6分
∴所求橢圓C的方程為![]() . 7分;
. 7分;
(Ⅱ)由(Ⅰ)知點(diǎn)A(-2,0),點(diǎn)B為(0,-1),設(shè)點(diǎn)P的坐標(biāo)為![]() 則
則![]() ,
,![]() ,由
,由![]() -4得-
-4得-![]() ,
,
∴點(diǎn)P的軌跡方程為![]() 9分
9分
設(shè)點(diǎn)B關(guān)于P的軌跡的對稱點(diǎn)為![]() ,則由軸對稱的性質(zhì)可得:
,則由軸對稱的性質(zhì)可得:![]() ,
,
解得:![]() , 11分
, 11分
∵點(diǎn)![]() 在橢圓上,∴
在橢圓上,∴![]() ,整理得
,整理得![]() 解得
解得![]() 或
或![]()
∴點(diǎn)P的軌跡方程為![]() 或
或![]() , 13分
, 13分
經(jīng)檢驗(yàn)![]() 和
和![]() 都符合題設(shè),
都符合題設(shè),
∴滿足條件的點(diǎn)P的軌跡方程為![]() 或
或![]() . 14分
. 14分



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
 (2009•杭州二模)如圖,在直角坐標(biāo)系xOy中,銳角△ABC內(nèi)接于圓x2+y2=1.已知BC平行于x軸,AB所在直線方程為y=kx+m(k>0),記角A,B,C所對的邊分別是a,b,c.
(2009•杭州二模)如圖,在直角坐標(biāo)系xOy中,銳角△ABC內(nèi)接于圓x2+y2=1.已知BC平行于x軸,AB所在直線方程為y=kx+m(k>0),記角A,B,C所對的邊分別是a,b,c.| 2ac |
| a2+c2-b2 |
| A+C |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
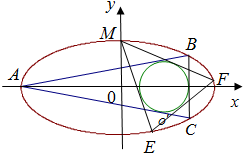 如圖,在直角坐標(biāo)系中,中心在原點(diǎn),焦點(diǎn)在X軸上的橢圓G的離心率為e=
如圖,在直角坐標(biāo)系中,中心在原點(diǎn),焦點(diǎn)在X軸上的橢圓G的離心率為e=
| ||
| 4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 (2013•石景山區(qū)二模)如圖,在直角坐標(biāo)系xOy中,角α的頂點(diǎn)是原點(diǎn),始邊與x軸正半軸重合,終邊交單位圓于點(diǎn)A,且α∈(
(2013•石景山區(qū)二模)如圖,在直角坐標(biāo)系xOy中,角α的頂點(diǎn)是原點(diǎn),始邊與x軸正半軸重合,終邊交單位圓于點(diǎn)A,且α∈(| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
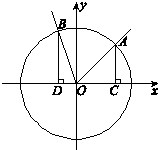 如圖,在直角坐標(biāo)系xOy中,角α的頂點(diǎn)是原點(diǎn),始邊與x軸正半軸重合,終邊交單位圓于點(diǎn)A,且α∈(
如圖,在直角坐標(biāo)系xOy中,角α的頂點(diǎn)是原點(diǎn),始邊與x軸正半軸重合,終邊交單位圓于點(diǎn)A,且α∈(| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,在直角坐標(biāo)系中,已知射線OA:x-y=0(x≥0),OB:
如圖,在直角坐標(biāo)系中,已知射線OA:x-y=0(x≥0),OB:| 3 |
| AP |
| PB |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com