
【題目】命題“奇函數的圖像關于原點對稱”的否命題是__________.
科目:高中數學 來源: 題型:
【題目】算法的三種基本結構是( )
A. 順序結構、模塊結構、條件結構 B. 順序結構、循環結構、模塊結構
C. 順序結構、條件結構、循環結構 D. 模塊結構、條件結構、循環結構
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學生在開學季準備銷售一種文具套盒進行試創業,在一個開學季內,每售出![]() 盒該產品獲利潤
盒該產品獲利潤![]() 元;未售出的產品,每盒虧損
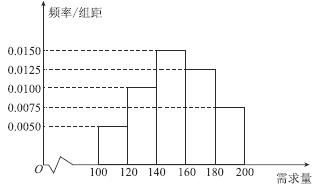
元;未售出的產品,每盒虧損![]() 元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示,該同學為這個開學季購進了
元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示,該同學為這個開學季購進了![]() 盒該產品,以
盒該產品,以![]() (單位:盒,
(單位:盒, ![]() )表示這個開學季內的市場需求量,(單位:元)表示這個開學季內經銷該產品的利潤.
)表示這個開學季內的市場需求量,(單位:元)表示這個開學季內經銷該產品的利潤.
(1)根據直方圖估計這個開學季內市場需求量![]() 的中位數;
的中位數;
(2)將![]() 表示為
表示為![]() 的函數;
的函數;
(3)根據直方圖估計利潤不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地建一座橋,兩端的橋墩已建好,這兩墩相距![]() 米,余下工程只需要建兩端橋墩之間的橋面和橋墩,經預測,一個橋墩的工程費用為256萬元,距離為
米,余下工程只需要建兩端橋墩之間的橋面和橋墩,經預測,一個橋墩的工程費用為256萬元,距離為![]() 米的相鄰兩墩之間的橋面工程費用為
米的相鄰兩墩之間的橋面工程費用為![]() 萬元。假設橋墩等距離分布,所有橋墩都視為點,且不考慮其他因素,記余下工程的費用為
萬元。假設橋墩等距離分布,所有橋墩都視為點,且不考慮其他因素,記余下工程的費用為![]() 萬元. 假設需要新建n個橋墩.
萬元. 假設需要新建n個橋墩.
(1)寫出n關于![]() 的函數關系式;
的函數關系式;
(2)試寫出![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(3)當![]() =640米時,需新建多少個橋墩才能使
=640米時,需新建多少個橋墩才能使![]() 最小?
最小?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某租賃公司擁有汽車100輛,當每輛車的月租金為3000元時,可全部租出.若每輛車的月租金每增加50元,未租出的車將會增加一輛,租出的車每輛每月需要維護費150元,未租出的車每輛每月需要維護費50元.
(1)當每輛車的月租金定位3600元時,能租出多少輛車?
(2)當每輛車的月租金定位多少元時,租賃公司的月收益最大,最大月收益是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在區間[-1,4]上有最大值10和最小值1.設
在區間[-1,4]上有最大值10和最小值1.設![]()
(1)求![]() 的值;
的值;
(2)證明:函數![]() 在
在![]() 上是增函數.
上是增函數.
(3)若不等式![]()
![]() 在
在![]() 上有解,求實數
上有解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 滿足以下兩個條件:
滿足以下兩個條件:
①不等式![]() 的解集是
的解集是![]() ;②函數
;②函數![]() 在
在![]() 上的最小值是3.
上的最小值是3.
(1)求![]() 的解析式;
的解析式;
(2)若點![]() (
(![]() )在函數
)在函數![]() 的圖象上,且
的圖象上,且![]() .
.
(i)求證:數列![]() 為等比數列;
為等比數列;
(ii)令![]() ,是否存在正整數
,是否存在正整數![]() ,使得
,使得![]() 取到最小值?若有,請求出
取到最小值?若有,請求出![]() 的值;若無,請說明理由.
的值;若無,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 的定義域為D,如果
的定義域為D,如果![]() ,使得
,使得![]() 成立,則稱函數
成立,則稱函數![]() 為“Ω函數”. 給出下列四個函數:①
為“Ω函數”. 給出下列四個函數:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() , 則其中“Ω函數”共有( )
, 則其中“Ω函數”共有( )
A.1個 B.2個 C.3個 D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com