
【題目】在直角坐標系xOy中,曲線C:x2=6y與直線l:y=kx+3交于M,N兩點.
(1)設M,N到y軸的距離分別為d1,d2,證明:d1d2為定值.
(2)y軸上是否存在點P,使得當k變動時,總有∠OPM=∠OPN?若存在,求以線段OP為直徑的圓的方程;若不存在,請說明理由.
【答案】(1)見解析; (2)![]() .
.
【解析】
(1)設點M(x1,y1)、N(x2,y2),將直線l的方程與曲線C的方程聯立,列出韋達定理,結合距離公式可證明題中結論;(2)設P(0,b)為符合題意的點,利用兩點的斜率公式結合韋達定理計算直線PM與直線PN的斜率之和為0,得出b的值,從而證明點P的存在性.
(1)將直線l的方程與曲線C的方程聯立![]() ,消去y并整理得x2﹣6kx﹣18=0.
,消去y并整理得x2﹣6kx﹣18=0.
設點M(x1,y1)、N(x2,y2),則x1x2=﹣18.
從而d1d2=|x1||x2|=|x1x2|=18(定值);
(2)存在符合題意的點,證明如下:設P(0,b)為符合題意的點,直線PM、PN的斜率分別為k1、k2,
從而![]() =
=![]() .
.
當b=﹣3時,有k1+k2=0,則直線PM的傾斜角與直線PN的傾斜角互補.
故∠OPM=∠OPN,所以點P(0,﹣3)符合題意.
故以線段OP為直徑的圓的方程為![]() .
.


 高中必刷題系列答案
高中必刷題系列答案科目:高中數學 來源: 題型:
【題目】如圖,一個湖的邊界是圓心為O的圓,湖的一側有一條直線型公路l,湖上有橋AB(AB是圓O的直徑).規劃在公路l上選兩個點P、Q,并修建兩段直線型道路PB、QA.規劃要求:線段PB、QA上的所有點到點O的距離均不小于圓O的半徑.已知點A、B到直線l的距離分別為AC和BD(C、D為垂足),測得AB=10,AC=6,BD=12(單位:百米).

(1)若道路PB與橋AB垂直,求道路PB的長;
(2)在規劃要求下,P和Q中能否有一個點選在D處?并說明理由;
(3)對規劃要求下,若道路PB和QA的長度均為d(單位:百米).求當d最小時,P、Q兩點間的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一臺機器生產某種產品,如果生產出一件甲等品可獲利50元,生產出一件乙等品可獲利30元,生產出一件次品,要賠20元,已知這臺機器生產出甲等品、乙等品和次品的概率分別為0.6,0.3,和0.1,則這臺機器每生產一件產品平均預期可獲利________元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有關部門要了解甲型H1N1流感預防知識在學校的普及情況,命制了一份有10道題的問卷到各學校做問卷調查.某中學A、B兩個班各被隨機抽取5名學生接受問卷調查,A班5名學生得分為:5、8、9、9、9,B班5名學生得分為:6、7、8、9、10.
(1)請你判斷A、B兩個班中哪個班的問卷得分要穩定一些,并說明你的理由;
(2)求如果把B班5名學生的得分看成一個總體,并用簡單隨機抽樣方法從中抽取樣本容量為2的樣本,求樣本平均數與總體平均數之差的絕對值不小于1的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是拋物線
是拋物線![]() 的焦點,點
的焦點,點![]() 是拋物線上的定點,且
是拋物線上的定點,且![]() .
.
![]() 求拋物線
求拋物線![]() 的方程;
的方程;
![]() 直線
直線![]() 與拋物線
與拋物線![]() 交于不同兩點
交于不同兩點![]() ,
,![]() ,直線AB與切線l平行,設切點為N點,試問
,直線AB與切線l平行,設切點為N點,試問![]() 的面積是否是定值,若是,求出這個定值;若不是,請說明理由.
的面積是否是定值,若是,求出這個定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠銷售部以箱為單位銷售某種零件,每箱的定價為200元,低于100箱按原價銷售;不低于100箱通過雙方議價,買方能以優惠![]() 成交的概率為0.6,以優惠
成交的概率為0.6,以優惠![]() 成交的概率為0.4.
成交的概率為0.4.
(1)甲、乙兩單位都要在該廠購買150箱這種零件,兩單位各自達成的成交價相互獨立,求甲單位優惠比例不低于乙單位優惠比例的概率;
(2)某單位需要這種零件650箱,求購買總價![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于四面體ABCD,給出下列四個命題:
①若AB=AC,BD=CD,則BC⊥AD; ②若AB=CD,AC=BD,則BC⊥AD;
③若AB⊥AC,BD⊥CD,則BC⊥AD;④若AB⊥CD,AC⊥BD,則BC⊥AD;
其中正確的命題的序號是( )
A.①②B.②③C.②④D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】計算機在數據處理時使用的是二進制,例如十進制數1,2,3,4的二進制數分別表示為1,10,11,100,二進制數…![]() 化為十進制數的公式為…
化為十進制數的公式為…![]()
![]() ,例如二進制數11等于十進制數
,例如二進制數11等于十進制數![]() ,又如二進制數101等于十進制數
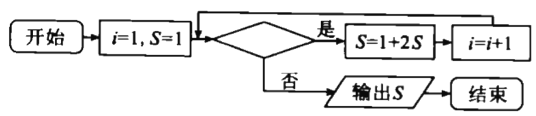
,又如二進制數101等于十進制數![]() ,下圖是某同學設計的將二進制數11111化為十進制數的程序框圖,則判斷框內應填入的條件是( )
,下圖是某同學設計的將二進制數11111化為十進制數的程序框圖,則判斷框內應填入的條件是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com