
【題目】如圖,已知圓錐![]() 和圓柱
和圓柱![]() 的組合體(它們的底面重合),圓錐的底面圓
的組合體(它們的底面重合),圓錐的底面圓![]() 半徑為
半徑為![]() ,
, ![]() 為圓錐的母線,
為圓錐的母線, ![]() 為圓柱
為圓柱![]() 的母線,
的母線, ![]() 為下底面圓
為下底面圓![]() 上的兩點,且
上的兩點,且![]() ,
, ![]() ,
, ![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)見解析(2)![]()
【解析】試題分析:(1)先根據平幾知識計算得![]() ,再根據圓柱性質得
,再根據圓柱性質得![]() 平面
平面![]() ,即有
,即有![]() ,最后根據線面垂直判定定理得
,最后根據線面垂直判定定理得![]() 平面
平面![]() ,即得平面
,即得平面![]() 平面
平面![]() ;(2)求二面角,一般利用空間向量進行求解,先根據條件建立空間直角坐標系,設立各點坐標,利用方程組解出各面法向量,利用向量數量積求法向量夾角,最后根據二面角與向量夾角之間關系求解
;(2)求二面角,一般利用空間向量進行求解,先根據條件建立空間直角坐標系,設立各點坐標,利用方程組解出各面法向量,利用向量數量積求法向量夾角,最后根據二面角與向量夾角之間關系求解
試題解析:解:(1)依題易知,圓錐的高為![]() ,又圓柱的高為
,又圓柱的高為![]() ,
,
所以![]() ,
,
因為![]() ,所以
,所以![]() ,
,
連接![]() ,易知
,易知![]() 三點共線,
三點共線, ![]() ,
,
所以![]() ,
,
所以![]() ,
,
解得![]() ,又因為
,又因為![]() ,圓
,圓![]() 的直徑為10,圓心
的直徑為10,圓心![]() 在
在![]() 內,
內,
所以易知![]() ,所以
,所以![]() .
.
因為![]() 平面
平面![]() ,所以
,所以![]() ,因為
,因為![]() ,所以
,所以![]() 平面
平面![]() .
.
又因為![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)如圖,以![]() 為原點,
為原點, ![]() 、
、![]() 所在的直線為
所在的直線為![]() 軸,建立空間直角坐標系.
軸,建立空間直角坐標系.
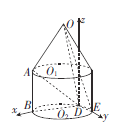
則![]() .
.
所以![]() ,
,
設平面![]() 的法向理為
的法向理為![]() ,
,
所以![]() ,令
,令![]() ,則
,則![]() .
.
可取平面![]() 的一個法向量為
的一個法向量為![]() ,
,
所以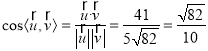 ,
,
所以二面角![]() 的正弦值為
的正弦值為![]() .
.


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:高中數學 來源: 題型:
【題目】某花店每天以每枝5元的價格從花市購進若干枝玫瑰花,然后以每枝10元的價格出售.如果當天賣不完,剩下的玫瑰花作垃圾處理.
(1)若花店一天購進17支玫瑰花,求當天的利潤![]() (單位:元),關于當天需求量
(單位:元),關于當天需求量![]() (單位:枝,
(單位:枝, ![]() 的解析式;
的解析式;
(2)花店記錄了100天玫瑰花的日需求量(單位:枝),整理得如表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
頻數 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①假設花店在這100天內每天購進16枝玫瑰花或每天購進17枝玫瑰花,分別計算這100天花店的日利潤(單位:元)的平均數,并以此作為決策依據,花店在這100天內每天購進16枝還是17枝玫瑰花?
②若花店一天購進17枝玫瑰花,以100天記錄的各需求量的頻率作為概率,求當天的利潤不少于75元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)是定義在R上的減函數,且f(x)>0恒成立,若對任意的x,y∈R,都有f(x﹣y)= ![]() ,
,
(1)求f(0)的值,并證明對任意的x,y∈R,f(x+y)=f(x)f(y);
(2)若f(﹣1)=3,解不等式 ![]() ≤9.
≤9.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設定義在R上的偶函數f(x)滿足f(x+2)=f(x),f′(x)是f(x)的導函數,當x∈[0,1]時,0≤f(x)≤1;當x∈(0,2)且x≠1時,x(x﹣1)f′(x)<0.則方程f(x)=lg|x|根的個數為( )
A.12
B.1 6
C.18
D.20
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中,正確的是 . (填序號)
①若集合A={x|kx2+4x+4=0}中只有一個元素,則k=1;
②在同一平面直角坐標系中,y=2x與y=2﹣x的圖象關于y軸對稱;
③y=( ![]() )﹣x是增函數;
)﹣x是增函數;
④定義在R上的奇函數f(x)有f(x)f(﹣x)≤0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩個命題p:x∈R,sinx+cosx>m恒成立,q:x∈R,y=(2m2﹣m)x為增函數.若p∨q為真命題,p∧q為假命題,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為提高市場銷售業績,某公司設計兩套產品促銷方案(方案1運作費用為![]() 元/件;方案2的的運作費用為
元/件;方案2的的運作費用為![]() 元/件),并在某地區部分營銷網點進行試點(每個試點網點只采用一種促銷方案),運作一年后,對比該地區上一年度的銷售情況,分別統計相應營銷網點個數,制作相應的列聯表如下表所示.
元/件),并在某地區部分營銷網點進行試點(每個試點網點只采用一種促銷方案),運作一年后,對比該地區上一年度的銷售情況,分別統計相應營銷網點個數,制作相應的列聯表如下表所示.
無促銷活動 | 采用促銷方案1 | 采用促銷方案2 | ||
本年度平均銷售額不高于上一年度平均銷售額 | 48 | 11 | 31 | 90 |
本年度平均銷售額高于上一年度平均銷售額 | 52 | 69 | 29 | 150 |
100 | 80 | 60 |
(Ⅰ)請根據列聯表提供的信息,為該公司今年選擇一套較為有利的促銷方案(不必說明理由);
(Ⅱ)已知該公司產品的成本為10元/件(未包括促銷活動運作費用),為制定本年度該地區的產品銷售價格,統計上一年度的![]() 組售價
組售價![]() (單位:元/件,整數)和銷量
(單位:元/件,整數)和銷量![]() (單位:件)(
(單位:件)(![]() )如下表所示:
)如下表所示:
售價 |
|
|
|
|
|
|
|
|
銷量 |
|
|
|
|
|
|
|
|
(ⅰ)請根據下列數據計算相應的相關指數![]() ,并根據計算結果,選擇合適的回歸模型進行擬合;
,并根據計算結果,選擇合適的回歸模型進行擬合;
(ⅱ)根據所選回歸模型,分析售價![]() 定為多少時?利潤
定為多少時?利潤![]() 可以達到最大.
可以達到最大.
|
|
| |
|
|
|
|
|
| ||
參考公式:相關指數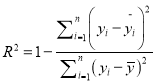 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com