
【題目】奇函數f(x)在R上存在導數![]() ,當x<0時,
,當x<0時,![]()
![]() f(x),則使得(x2﹣1)f(x)<0成立的x的取值范圍為( )
f(x),則使得(x2﹣1)f(x)<0成立的x的取值范圍為( )
A.(﹣1,0)∪(0,1)B.(﹣∞,﹣1)∪(0,1)
C.(﹣1,0)∪(1,+∞)D.(﹣∞,﹣1)∪(1,+∞)
 走進文言文系列答案
走進文言文系列答案科目:高中數學 來源: 題型:
【題目】已知函數h(x)是定義在(﹣2,2)上,滿足h(﹣x)=﹣h(x),且x∈(0,2)時,h(x)=﹣2x,當x∈(﹣2,0)時,不等式[h(x)+2]2>h(x)m﹣1恒成立,則實數m的取值范圍是_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() x3(a>0且a≠1).
x3(a>0且a≠1).
(1)求函數f(x)的定義域;
(2)討論函數f(x)的奇偶性;
(3)求a的取值范圍,使f(x)>0在定義域上恒成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣ax+1(a∈R).
(1)求f(x)的單調區間;
(2)設g(x)=lnx![]() ,若對任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求實數a的取值范圍.
,若對任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,左、右焦點分別是
,左、右焦點分別是![]() ,橢圓
,橢圓![]() 上短軸的一個端點與兩個焦點構成的三角形的面積為
上短軸的一個端點與兩個焦點構成的三角形的面積為![]() ;
;
(1)求橢圓![]() 的方程;
的方程;
(2)過![]() 作垂直于
作垂直于![]() 軸的直線
軸的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點(點
兩點(點![]() 在第二象限),
在第二象限),![]() 是橢圓上位于直線
是橢圓上位于直線![]() 兩側的動點,若
兩側的動點,若![]() ,求證:直線
,求證:直線![]() 的斜率為定值.
的斜率為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知公差不為零的等差數列![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比數列,
成等比數列,
(1)求數列![]() 的通項公式;
的通項公式;
(2)數列![]() 滿足
滿足![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() ,若不等式
,若不等式![]() 對一切
對一切![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
(3)設數列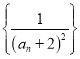 的前n項和為
的前n項和為![]() ,求證:對任意正整數n,都有
,求證:對任意正整數n,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古希臘雅典學派算學家歐道克薩斯提出了“黃金分割”的理論,利用尺規作圖可畫出己知線段的黃金分割點,具體方法如下:(l)取線段AB=2,過點B作AB的垂線,并用圓規在垂線上截取BC=![]() AB,連接AC;(2)以C為圓心,BC為半徑畫弧,交AC于點D;(3)以A為圓心,以AD為半徑畫弧,交AB于點E.則點E即為線段AB的黃金分割點.若在線段AB上隨機取一點F,則使得BE≤AF≤AE的概率約為( )(參考數據:
AB,連接AC;(2)以C為圓心,BC為半徑畫弧,交AC于點D;(3)以A為圓心,以AD為半徑畫弧,交AB于點E.則點E即為線段AB的黃金分割點.若在線段AB上隨機取一點F,則使得BE≤AF≤AE的概率約為( )(參考數據:![]() 2.236)
2.236)
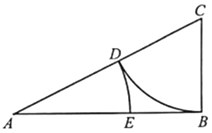
A. 0.236B. 0.382C. 0.472D. 0.618
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com