
【題目】設橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,下頂點為
,下頂點為![]() ,橢圓
,橢圓![]() 的離心率是
的離心率是![]() ,
,![]() 的面積是
的面積是![]() .
.
(1)求橢圓![]() 的標準方程.
的標準方程.
(2)直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點(異于
兩點(異于![]() 點),若直線
點),若直線![]() 與直線
與直線![]() 的斜率之和為1,證明:直線
的斜率之和為1,證明:直線![]() 恒過定點,并求出該定點的坐標.
恒過定點,并求出該定點的坐標.
科目:高中數學 來源: 題型:
【題目】如圖,在多面體![]() 中,梯形
中,梯形![]() 與平行四邊形
與平行四邊形![]() 所在平面互相垂直,
所在平面互相垂直, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
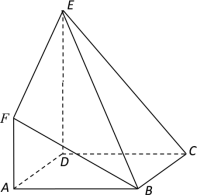
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)判斷線段![]() 上是否存在點
上是否存在點![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求 出
?若存在,求 出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據某水文觀測點的歷史統計數據,得到某河流水位![]() (單位:米)的頻率分布直方圖如下.將河流水位在
(單位:米)的頻率分布直方圖如下.將河流水位在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 各段內的頻率作為相應段的概率,并假設每年河流水位變化互不影響.
各段內的頻率作為相應段的概率,并假設每年河流水位變化互不影響.
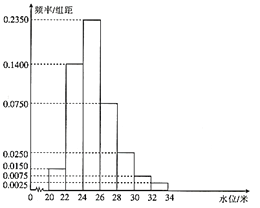
(1)求未來4年中,至少有2年該河流水位![]() 的概率(結果用分數表示).
的概率(結果用分數表示).
(2)已知該河流對沿河![]() 工廠的影響如下:當
工廠的影響如下:當![]() 時,不會造成影響;當
時,不會造成影響;當![]() 時,損失50000元;當
時,損失50000元;當![]() 時,損失300000元.為減少損失,
時,損失300000元.為減少損失,![]() 工廠制定了三種應對方案.
工廠制定了三種應對方案.
方案一:不采取措施;
方案二:防御不超過30米的水位,需要工程費用8000元;
方案三:防御34米的最高水位,需要工程費用20000元.
試問哪種方案更好,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體![]() 中,點E是棱
中,點E是棱![]() 的中點,點F是線段
的中點,點F是線段![]() 上的一個動點.有以下三個命題:
上的一個動點.有以下三個命題:
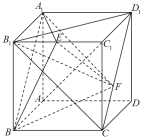
①異面直線![]() 與
與![]() 所成的角是定值;
所成的角是定值;
②三棱錐![]() 的體積是定值;
的體積是定值;
③直線![]() 與平面
與平面![]() 所成的角是定值.
所成的角是定值.
其中真命題的個數是( )
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(I)求函數![]() 的對稱軸方程;
的對稱軸方程;
(II)將函數![]() 的圖象上各點的縱坐標保持不變,橫坐標伸長為原來的2倍,然后再向左平移
的圖象上各點的縱坐標保持不變,橫坐標伸長為原來的2倍,然后再向左平移![]() 個單位,得到函數
個單位,得到函數![]() 的圖象.若
的圖象.若![]() 分別是△ABC三個內角A,B,C的對邊,a=2,c=4,且
分別是△ABC三個內角A,B,C的對邊,a=2,c=4,且![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
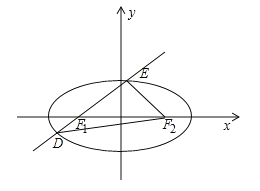
【題目】如圖,已知橢圓![]() ,
,![]() 分別為其左、右焦點,過
分別為其左、右焦點,過![]() 的直線與此橢圓相交于
的直線與此橢圓相交于![]() 兩點,且
兩點,且![]() 的周長為8,橢圓
的周長為8,橢圓![]() 的離心率為
的離心率為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)在平面直角坐標系![]() 中,已知點
中,已知點![]() 與點
與點![]() ,過
,過![]() 的動直線
的動直線![]() (不與
(不與![]() 軸平行)與橢圓相交于
軸平行)與橢圓相交于![]() 兩點,點
兩點,點![]() 是點
是點![]() 關于
關于![]() 軸的對稱點.求證:
軸的對稱點.求證:
(i)![]() 三點共線.
三點共線.
(ii)![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
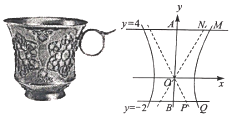
【題目】如圖為陜西博物館收藏的國寶——唐·金筐寶鈿團花紋金杯,杯身曲線內收,玲瓏嬌美,巧奪天工,是唐代金銀細作的典范之作.該杯型幾何體的主體部分可近似看作是雙曲線![]() 的右支與直線
的右支與直線![]() ,
,![]() ,
,![]() 圍成的曲邊四邊形
圍成的曲邊四邊形![]() 繞
繞![]() 軸旋轉一周得到的幾何體,如圖
軸旋轉一周得到的幾何體,如圖![]() 分別為
分別為![]() 的漸近線與
的漸近線與![]() ,
,![]() 的交點,曲邊五邊形
的交點,曲邊五邊形![]() 繞
繞![]() 軸旋轉一周得到的幾何體的體積可由祖恒原理(祖恒原理:冪勢既同,則積不容異).意思是:兩等高的幾何體在同高處被截得的兩截面面積均相等,那么這兩個幾何體的體積相等,那么這兩個幾何體的體積相等),據此求得該金杯的容積是_____.(杯壁厚度忽略不計)
軸旋轉一周得到的幾何體的體積可由祖恒原理(祖恒原理:冪勢既同,則積不容異).意思是:兩等高的幾何體在同高處被截得的兩截面面積均相等,那么這兩個幾何體的體積相等,那么這兩個幾何體的體積相等),據此求得該金杯的容積是_____.(杯壁厚度忽略不計)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com