Question

【題目】某物流公司購買了一塊長AM＝30米，寬AN＝20米的矩形地塊，計劃把圖中矩形ABCD建設為倉庫，其余地方為道路和停車場，要求頂點C在地塊對角線MN上，B、D分別在邊AM、AN上，假設AB的長度為x米

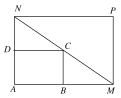
(1)求矩形ABCD的面積S關于x的函數解析式；

(2)要使倉庫占地ABCD的面積不少于144平方米，則AB的長度應在什么范圍內？

Answer 1

【答案】(1) S＝20x－x2(0<x<30)(2)[12,18]．

【解析】

(1) 根據三角形相似，利用x表示出AD，進而用x表示出矩形ABCD的面積。

(2) 根據面積不小于144平方米，列出一元二次不等式，解不等式即可。

(1)根據題意，得△NDC與△NAM相似，所以，即，解得AD＝20－x.

所以矩形ABCD的面積S關于x的函數為S＝20x－x2(0<x<30)．

(2)要使倉庫占地ABCD的面積不少于144平方米，即20x－x2≥144，化簡得x2－30x＋216≤0，解得12≤x≤18，所以AB的長度的取值范圍為[12,18]．