
【題目】已知函數![]() .
.
(1)若![]() ,求函數
,求函數![]() 的極值;
的極值;
(2)若![]() 在
在![]() 內為單調增函數,求實數
內為單調增函數,求實數![]() 的取值范圍;
的取值范圍;
(3)對于![]() ,求證:
,求證: ![]() .
.
 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線![]() 的參數方程為
的參數方程為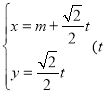 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .且曲線
.且曲線![]() 的左焦點
的左焦點![]() 在直線
在直線![]() 上.
上.
(1)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值;
的值;
(2)求曲線![]() 的內接矩形的周長的最大值.
的內接矩形的周長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】化為推出一款6寸大屏手機,現對500名該手機使用者(200名女性,300名男性)進行調查,對手機進行打分,打分的頻數分布表如下:
女性用戶:
分值區(qū)間 |
|
|
|
|
|
頻數 | 20 | 40 | 80 | 50 | 10 |
分值區(qū)間 |
|
|
|
|
|
頻數 | 45 | 75 | 90 | 60 | 30 |
男性用戶:
(1)如果評分不低于70分,就表示該用戶對手機“認可”,否則就表示“不認可”,完成下列![]() 列聯表,并回答是否有
列聯表,并回答是否有![]() 的把握認為性別對手機的“認可”有關:
的把握認為性別對手機的“認可”有關:
女性用戶 | 男性用戶 | 合計 | |
“認可”手機 | |||
“不認可”手機 | |||
合計 |
附:
| 0.05 | 0.01 |
| 3.841 | 6635 |
![]()
(2)根據評分的不同,運用分層抽樣從男性用戶中抽取20名用戶,在這20名用戶中,從評分不低于80分的用戶中任意抽取3名用戶,求3名用戶中評分小于90分的人數的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() +
+![]() =1(a>b>0)的左焦點為F,右頂點為A,拋物線y2=
=1(a>b>0)的左焦點為F,右頂點為A,拋物線y2=![]() (a+c)x與橢圓交于B,C兩點,若四邊形ABFC是菱形,則橢圓的離心率等于( )
(a+c)x與橢圓交于B,C兩點,若四邊形ABFC是菱形,則橢圓的離心率等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=x2-4|x|-5.
(Ⅰ)畫出y=f(x)的圖象;
(Ⅱ)設A={x|f(x)≥7},求集合A;
(Ⅲ)方程f(x)=k+1有兩解,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln x+![]() +ax(a是實數),g(x)=
+ax(a是實數),g(x)=![]() +1.
+1.
(1)當a=2時,求函數f(x)在定義域上的最值;
(2)若函數f(x)在[1,+∞)上是單調函數,求a的取值范圍;
(3)是否存在正實數a滿足:對于任意x1∈[1,2],總存在x2∈[1,2],使得f(x1)=g(x2)成立? 若存在,求出a的取值范圍,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知右焦點為![]() 的橢圓
的橢圓![]() 關于直線
關于直線![]() 對稱的圖形過坐標原點.
對稱的圖形過坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 且不垂直于
且不垂直于![]() 軸的直線與橢圓
軸的直線與橢圓![]() 交于
交于![]() ,
,![]() 兩點,點
兩點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,證明:直線
,證明:直線![]() 與
與![]() 軸的交點為
軸的交點為![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com