
【題目】如圖,已知四棱錐P﹣ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC= ![]() AB=
AB= ![]() ,平面PBC⊥平面ABCD.
,平面PBC⊥平面ABCD. 
(1)求證:AC⊥PB;
(2)若PB=PC= ![]() ,問在側(cè)棱PB上是否存在一點(diǎn)M,使得二面角M﹣AD﹣B的余弦值為
,問在側(cè)棱PB上是否存在一點(diǎn)M,使得二面角M﹣AD﹣B的余弦值為 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
【答案】
(1)證明:取AB的中點(diǎn)E,連結(jié)CE,
∵AB∥CD,DC= ![]() AB,∴DC
AB,∴DC ![]() AE,
AE,
∴四邊形AECD是平行四邊形,
又∵∠ADC=90°,∴四邊形AECD是正方形,∴CE⊥AB,
∴△CAB是等腰三角開有,且CA=CB=2,AB=2 ![]() ,
,
∴AC2+CB2=AB2,∴AC⊥CB,
又∵平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,
∴AC⊥平面PBC,
又PB平面PBC,∴AC⊥PB
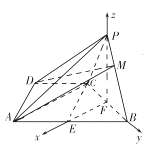
(2)解:設(shè)BC的中點(diǎn)為F,連結(jié)PF,
∵PB=PC,∴PF=BC,
∴PF⊥平面ABCD,∴PF⊥AC,
連結(jié)EF,則EF∥AC,∴PF⊥FE,EF⊥BC,
分別以FE、FB、FP所在的直線為x軸,y軸,z軸,建立空間直角坐標(biāo)系,
∵AD=PB=PC= ![]() ,則F(0,0,0),A(2,﹣1,0),
,則F(0,0,0),A(2,﹣1,0),
B(0,1,0),D(1,﹣2,0),P(0,0,1),
∴ ![]() =(0,1,﹣1),
=(0,1,﹣1), ![]() =(﹣1,﹣1,0),
=(﹣1,﹣1,0), ![]() =(0,0,1),
=(0,0,1),
若在線段PB上存在一點(diǎn)M,設(shè) ![]() =
= ![]() ,(0≤λ<1),
,(0≤λ<1),
∵ ![]() ,∴
,∴ ![]() =λ(0,1,﹣1)+(0,0,1)=(0,λ,1﹣λ),
=λ(0,1,﹣1)+(0,0,1)=(0,λ,1﹣λ),
∴M(0,λ,1﹣λ), ![]() ,
,
設(shè)平面MAD的一個(gè)法向量 ![]() =(x,y,z),
=(x,y,z),
則 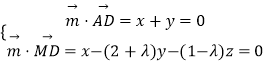 ,取x=1,得
,取x=1,得 ![]() =(1,﹣1,
=(1,﹣1, ![]() ),
),
平面ABCD的法向量 ![]() =(0,0,1),
=(0,0,1),
∵二面角M﹣AD﹣B的余弦值為 ![]() ,
,
∴|cos< ![]() >|=
>|= ![]() =
=  =
= ![]() ,
,
解得 ![]() 或λ=2(舍).
或λ=2(舍).
∴存在點(diǎn)M,使得二面角M﹣AD﹣B的余弦值為 ![]() ,且
,且 ![]() =
= ![]() .
.
【解析】(1)取AB的中點(diǎn)E,連結(jié)CE,推導(dǎo)出四邊形AECD是正方形,從而CE⊥AB,再求出AC⊥CB,由此能證明AC⊥PB.(2)設(shè)BC的中點(diǎn)為F,連結(jié)PF,分別以FE、FB、FP所在的直線為x軸,y軸,z軸,建立空間直角坐標(biāo)系,利用向量法能求出結(jié)果.
【考點(diǎn)精析】利用空間中直線與直線之間的位置關(guān)系對(duì)題目進(jìn)行判斷即可得到答案,需要熟知相交直線:同一平面內(nèi),有且只有一個(gè)公共點(diǎn);平行直線:同一平面內(nèi),沒有公共點(diǎn);異面直線: 不同在任何一個(gè)平面內(nèi),沒有公共點(diǎn).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知命題![]() 方程
方程![]() 有兩個(gè)不等的實(shí)根;命題
有兩個(gè)不等的實(shí)根;命題![]() 方程
方程![]() 無實(shí)根,若“
無實(shí)根,若“![]() ”為真,“
”為真,“![]() ”為假,則實(shí)數(shù)
”為假,則實(shí)數(shù)![]() 的取值范圍為___________.(寫成區(qū)間的形式)
的取值范圍為___________.(寫成區(qū)間的形式)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,設(shè)拋物線![]() 的準(zhǔn)線
的準(zhǔn)線![]() 與
與![]() 軸交于橢圓
軸交于橢圓![]() 的右焦點(diǎn)
的右焦點(diǎn)![]() 為
為![]() 的左焦點(diǎn).橢圓的離心率為
的左焦點(diǎn).橢圓的離心率為![]() ,拋物線
,拋物線![]() 與橢圓
與橢圓![]() 交于
交于![]() 軸上方一點(diǎn)
軸上方一點(diǎn)![]() ,連接
,連接![]() 并延長(zhǎng)其交
并延長(zhǎng)其交![]() 于點(diǎn)
于點(diǎn)![]() ,
, ![]() 為
為![]() 上一動(dòng)點(diǎn),且在
上一動(dòng)點(diǎn),且在![]() 之間移動(dòng).
之間移動(dòng).
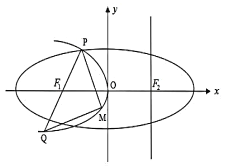
(1)當(dāng)![]() 取最小值時(shí),求
取最小值時(shí),求![]() 和
和![]() 的方程;
的方程;
(2)若![]() 的邊長(zhǎng)恰好是三個(gè)連續(xù)的自然數(shù),當(dāng)
的邊長(zhǎng)恰好是三個(gè)連續(xù)的自然數(shù),當(dāng)![]() 面積取最大值時(shí),求面積最大值以及此時(shí)直線
面積取最大值時(shí),求面積最大值以及此時(shí)直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓 C:![]() 的焦距為2,且過點(diǎn)
的焦距為2,且過點(diǎn)![]() ,右焦點(diǎn)為
,右焦點(diǎn)為![]() .設(shè)A,B 是C上的兩個(gè)動(dòng)點(diǎn),線段 AB 的中點(diǎn)M 的橫坐標(biāo)為
.設(shè)A,B 是C上的兩個(gè)動(dòng)點(diǎn),線段 AB 的中點(diǎn)M 的橫坐標(biāo)為![]() ,線段AB的中垂線交橢圓C于P,Q 兩點(diǎn).
,線段AB的中垂線交橢圓C于P,Q 兩點(diǎn).
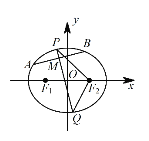
(1)求橢圓 C 的方程;
(2)設(shè)M點(diǎn)縱坐標(biāo)為m,求直線PQ的方程,并求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)h(x)=x2+ax+b在(0,1)上有兩個(gè)不同的零點(diǎn),記min{m,n}= ![]() ,則min{h(0),h(1)}的取值范圍為 .
,則min{h(0),h(1)}的取值范圍為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知焦點(diǎn)在![]() 軸上的橢圓
軸上的橢圓![]() 過點(diǎn)
過點(diǎn)![]() ,且離心率為
,且離心率為![]() .
.
(Ⅰ)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(Ⅱ)若直線![]() (
(![]() ,
,![]() )與橢圓C交于兩點(diǎn)A、B,點(diǎn)D滿足
)與橢圓C交于兩點(diǎn)A、B,點(diǎn)D滿足![]() ,經(jīng)過點(diǎn)D及點(diǎn)
,經(jīng)過點(diǎn)D及點(diǎn)![]() 的直線的斜率為
的直線的斜率為![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】圖是函數(shù)y=Asin(ωx+φ)(x∈R)在區(qū)間 ![]() 上的圖象,為了得到這個(gè)函數(shù)的圖象,只要將y=sinx(x∈R)的圖象上所有的點(diǎn)( )
上的圖象,為了得到這個(gè)函數(shù)的圖象,只要將y=sinx(x∈R)的圖象上所有的點(diǎn)( ) 
A.向左平移 ![]() 個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)縮短到原來的
個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)縮短到原來的 ![]() 倍,縱坐標(biāo)不變
倍,縱坐標(biāo)不變
B.向左平移 ![]() 個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)伸長(zhǎng)到原來的2倍,縱坐標(biāo)不變
個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)伸長(zhǎng)到原來的2倍,縱坐標(biāo)不變
C.向左平移 ![]() 個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)縮短到原來的
個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)縮短到原來的 ![]() 倍,縱坐標(biāo)不變
倍,縱坐標(biāo)不變
D.向左平移 ![]() 個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)伸長(zhǎng)到原來的2倍,縱坐標(biāo)不變
個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)伸長(zhǎng)到原來的2倍,縱坐標(biāo)不變
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分12分)
將邊長(zhǎng)為2的正方形ABCD沿對(duì)角線BD折疊,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=![]() .
.
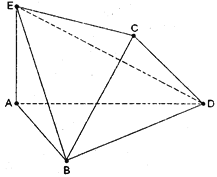
(Ⅰ)求證:DE⊥AC;
(Ⅱ)求DE與平面BEC所成角的正弦值;
(Ⅲ)直線BE上是否存在一點(diǎn)M,使得CM∥平面ADE,若存在,求點(diǎn)M的位置,不存在請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(12分)已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓C的長(zhǎng)軸長(zhǎng)為4.
,橢圓C的長(zhǎng)軸長(zhǎng)為4.
(1)求橢圓C的方程;
(2)已知直線![]() 與橢圓C交于A,B兩點(diǎn),是否存在實(shí)數(shù)k使得以線段AB 為直徑的圓恰好經(jīng)過坐標(biāo)原點(diǎn)O?若存在,求出k的值;若不存在,請(qǐng)說明理由.
與橢圓C交于A,B兩點(diǎn),是否存在實(shí)數(shù)k使得以線段AB 為直徑的圓恰好經(jīng)過坐標(biāo)原點(diǎn)O?若存在,求出k的值;若不存在,請(qǐng)說明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com