
【題目】(本小題滿分12分)
將邊長為2的正方形ABCD沿對角線BD折疊,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=![]() .
.
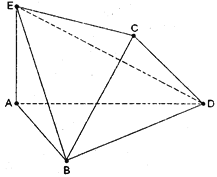
(Ⅰ)求證:DE⊥AC;
(Ⅱ)求DE與平面BEC所成角的正弦值;
(Ⅲ)直線BE上是否存在一點M,使得CM∥平面ADE,若存在,求點M的位置,不存在請說明理由.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】橢圓C: ![]() =1的右焦點F,過焦點F的直線l0⊥x軸,P(x0 , y0)(x0y0≠0)為C上任意一點,C在點P處的切線為l,l與l0相交于點M,與直線l1:x=3相交于N.
=1的右焦點F,過焦點F的直線l0⊥x軸,P(x0 , y0)(x0y0≠0)為C上任意一點,C在點P處的切線為l,l與l0相交于點M,與直線l1:x=3相交于N.
(I) 求證;直線 ![]() =1是橢圓C在點P處的切線;
=1是橢圓C在點P處的切線;
(Ⅱ)求證: ![]() 為定值,并求此定值;
為定值,并求此定值;
(Ⅲ)請問△ONP(O為坐標原點)的面積是否存在最小值?若存在,請求出最小及此時點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC= ![]() AB=
AB= ![]() ,平面PBC⊥平面ABCD.
,平面PBC⊥平面ABCD. 
(1)求證:AC⊥PB;
(2)若PB=PC= ![]() ,問在側棱PB上是否存在一點M,使得二面角M﹣AD﹣B的余弦值為
,問在側棱PB上是否存在一點M,使得二面角M﹣AD﹣B的余弦值為 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB⊥CD,AD∥BC,AD=3,BC=2AB=2,E,F分別在BC,AD上,EF∥AB.現將四邊形ABEF沿EF折起,使平面ABEF⊥平面EFDC.
(Ⅰ)若BE= ![]() ,在折疊后的線段AD上是否存在一點P,且
,在折疊后的線段AD上是否存在一點P,且 ![]() ,使得CP∥平面ABEF?若存在,求出λ的值,若不存在,說明理由;
,使得CP∥平面ABEF?若存在,求出λ的值,若不存在,說明理由;
(Ⅱ)求三棱錐A﹣CDF的體積的最大值,并求此時二面角E﹣AC﹣F的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】命題p:α∈R,sin(π﹣α)=cosα;命題q:“0<a<4”是“關于x的不等式ax2+ax+1>0的解集是實數集R”的充分必要條件,則下面結論正確的是( )
A.p是假命題
B.q是真命題
C.“p∧q”是假命題
D.“p∨q”是假命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,
若函數![]() 有唯一零點,則以下四個命題中正確的是______(填寫正確序號)
有唯一零點,則以下四個命題中正確的是______(填寫正確序號)
①.![]() ②.函數
②.函數![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 平行
平行
③.函數![]() 在
在![]() 上的最大值為
上的最大值為![]()
④.函數![]() 在
在 ![]() 上單調遞減
上單調遞減
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】連續拋擲同一顆均勻的骰子,令第i次得到的點數為ai , 若存在正整數k,使a1+a2+…+ak=6,則稱k為你的幸運數字.
(1)求你的幸運數字為3的概率;
(2)若k=1,則你的得分為5分;若k=2,則你的得分為3分;若k=3,則你的得分為1分;若拋擲三次還沒找到你的幸運數字則記0分,求得分X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】拋物線![]() 的焦點為
的焦點為![]() 上任一點
上任一點![]() 在
在![]() 軸上的射影為
軸上的射影為![]() 中點為
中點為![]() ,
,![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)直線![]() 過
過![]() 與
與![]() 從下到上依次交于
從下到上依次交于![]() ,與
,與![]() 交于
交于![]() ,直線
,直線![]() 過
過![]() 與
與![]() 從下到上依次交于
從下到上依次交于![]() ,與
,與![]() 交于
交于![]() ,
,![]() ,
,![]() 的斜率之積為
的斜率之積為![]() ,設
,設![]() 的面積分別為
的面積分別為![]() ,是否存在
,是否存在![]() 使得
使得![]() 成等比數列?若存在,求
成等比數列?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com