
【題目】某車間為了規定工時定額,需要確定加工零件所花費的時間,為此作了四次試驗,得到的數據如下:
零件的個數x(個) | 2 | 3 | 4 | 5 |
加工的時間y(小時) | 2.5 | 3 | 4 | 4.5 |

(1)在給定的坐標系中畫出表中數據的散點圖;
(2)求出y關于x的線性回歸方程![]() =bx+a,
=bx+a,
(3)試預測加工20個零件需要多少小時?
 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,一直一艘船由![]() 島以
島以![]() 海里/小時的速度往北偏東
海里/小時的速度往北偏東![]() 的
的![]() 島形式,計劃到達
島形式,計劃到達![]() 島后停留
島后停留![]() 分鐘后繼續以相同的速度駛往
分鐘后繼續以相同的速度駛往![]() 島.
島.![]() 島在
島在![]() 島的北偏西
島的北偏西![]() 的方向上,
的方向上,![]() 島也也在
島也也在![]() 島的北偏西
島的北偏西![]() 的方向上.上午
的方向上.上午![]() 時整,該船從
時整,該船從![]() 島出發.上午
島出發.上午![]() 時
時![]() 分,該船到達
分,該船到達![]() 處,此時測得
處,此時測得![]() 島在北偏西
島在北偏西![]() 的方向上.如果一切正常,此船何時能到達
的方向上.如果一切正常,此船何時能到達![]() 島?(精確到
島?(精確到![]() 分鐘)
分鐘)

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知曲線C的參數方程為 ![]() (α為參數),以直角坐標系原點O為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標軸方程為ρcos(θ﹣
(α為參數),以直角坐標系原點O為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標軸方程為ρcos(θ﹣ ![]() )=2
)=2 ![]() .
.
(1)求曲線C的普通方程與直線l的直角坐標方程;
(2)設點P為曲線C上的動點,求點P到直線l距離的最大值及其對應的點P的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在原點![]() ,焦點在
,焦點在![]() 軸上,離心率為
軸上,離心率為![]() 的橢圓過點
的橢圓過點 .
.
(1)求橢圓的方程;
(2)設不過原點![]() 的直線
的直線![]() 與該橢圓交于
與該橢圓交于![]() 兩點,滿足直線
兩點,滿足直線![]() 的斜率依次成等比數列,求
的斜率依次成等比數列,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了了解一年內的用水情況,抽取了10天的用水量如下表所示:
天數 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/噸 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在這10天中,該公司用水量的平均數是多少?每天用水量的中位數是多少?
(Ⅱ)你認為應該用平均數和中位數中的哪一個數來描述該公司每天的用水量?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年4月23日“世界讀書日”來臨之際,某校為了了解中學生課外閱讀情況,隨機抽取了100名學生,并獲得了他們一周課外閱讀時間(單位:小時)的數據,整理得到數據分組及頻數分布表.
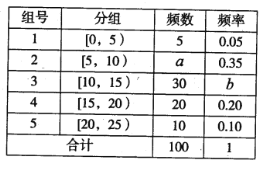
(Ⅰ)求![]() 的值,并作出這些數據的頻率分布直方圖;
的值,并作出這些數據的頻率分布直方圖;

(Ⅱ)假設每組數據組間是平均分布的,試估計該組數據的平均數;(同一組中的數據用該組區間的中點值作代表);
(Ⅲ)現從第3、4、5組中用分層抽樣的方法抽取6人參加校“中華詩詞比賽”,經過比賽后從這6人中選拔2人組成該校代表隊,求這2人來自不同組別的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設{an}和{bn}是兩個等差數列,記cn=max{b1-a1n,b2-a2n,…,bn-ann}(n=1,2,3,…),其中max{x1,x2,…,xs}表示x1,x2,…,xs這s個數中最大的數.
(Ⅰ)若an=n,bn=2n-1,求c1,c2,c3的值,并證明{cn}是等差數列;
(Ⅱ)證明:或者對任意正數M,存在正整數m,當n≥m時, ![]() >M;或者存在正整數m,使得cm,cm+1,cm+2,…是等差數列.
>M;或者存在正整數m,使得cm,cm+1,cm+2,…是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年4月23日“世界讀書日”來臨之際,某校為了了解中學生課外閱讀情況,隨機抽取了100名學生,并獲得了他們一周課外閱讀時間(單位:小時)的數據,整理得到數據分組及頻數分布表.

(1)求![]() 的值,并作出這些數據的頻率分布直方圖;
的值,并作出這些數據的頻率分布直方圖;

(2)現從第3、4、5組中用分層抽樣的方法抽取6人參加校“中華詩詞比賽”,經過比賽后從這6人中選拔2人組成該校代表隊,求這2人來自不同組別的概率;
(3)假設每組數據組間是平均分布的,若該校希望使15%的學生的一周課外閱讀時間不低于![]() (小時)的時間,作為評選該校“課外閱讀能手”的依據,試估計該值
(小時)的時間,作為評選該校“課外閱讀能手”的依據,試估計該值![]() ,并說明理由.
,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(選修4﹣4:坐標系與參數方程)
已知曲線C1的參數方程為 ![]() (t為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρ=2sinθ.
(t為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρ=2sinθ.
(1)把C1的參數方程化為極坐標方程;
(2)求C1與C2交點的極坐標(ρ≥0,0≤θ<2π)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com