
【題目】某企業(yè)準備推出一種花卉植物用于美化城市環(huán)境,為評估花卉的生長水平,現(xiàn)對該花卉植株的高度(單位:厘米)進行抽查,所得數(shù)據(jù)分組為![]() ,據(jù)此制作的頻率分布直方圖如圖所示.
,據(jù)此制作的頻率分布直方圖如圖所示.
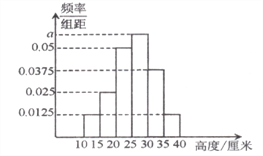
(1)求出直方圖中的![]() 值;
值;
(2)利用直方圖估算花卉植株高度的中位數(shù);
(3)若樣本容量為32,現(xiàn)準備從高度在![]() 的植株中繼續(xù)抽取2顆做進一步調(diào)查,求抽取植株來自同一組的概率.
的植株中繼續(xù)抽取2顆做進一步調(diào)查,求抽取植株來自同一組的概率.
 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若![]() 對定義域每的任意
對定義域每的任意![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅲ)證明:對于任意正整數(shù)![]() ,不等式
,不等式![]() 恒成立。
恒成立。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為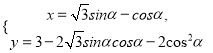 (
(![]() 為參數(shù)).以坐標原點為極點,以
為參數(shù)).以坐標原點為極點,以![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)當(dāng)![]() 時,求曲線
時,求曲線![]() 和曲線
和曲線![]() 的交點
的交點![]() 的直角坐標;
的直角坐標;
(2)當(dāng)![]() 時,設(shè)
時,設(shè)![]() ,
, ![]() 分別是曲線
分別是曲線![]() 與曲線
與曲線![]() 上動點,求
上動點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知集合![]() ,其中
,其中![]() ,由
,由![]() 中的元素構(gòu)成兩個相應(yīng)的集合:
中的元素構(gòu)成兩個相應(yīng)的集合:
![]() ,
, ![]() .
.
其中![]() 是有序數(shù)對,集合
是有序數(shù)對,集合![]() 和
和![]() 中的元素個數(shù)分別為
中的元素個數(shù)分別為![]() 和
和![]() .
.
若對于任意的![]() ,總有
,總有![]() ,則稱集合
,則稱集合![]() 具有性質(zhì)
具有性質(zhì)![]() .
.
(Ⅰ)檢驗集合![]() 與
與![]() 是否具有性質(zhì)
是否具有性質(zhì)![]() 并對其中具有性質(zhì)
并對其中具有性質(zhì)![]() 的集合,寫出相應(yīng)的集合
的集合,寫出相應(yīng)的集合![]() 和
和![]() .
.
(Ⅱ)對任何具有性質(zhì)![]() 的集合
的集合![]() ,證明
,證明![]() .
.
(Ⅲ)判斷![]() 和
和![]() 的大小關(guān)系,并證明你的結(jié)論.
的大小關(guān)系,并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標系中,以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,過點
,過點![]() 的直線
的直線![]() 的參數(shù)方程為
的參數(shù)方程為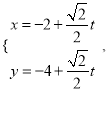 (
(![]() 為參數(shù)),直線
為參數(shù)),直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點.
兩點.
(Ⅰ)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
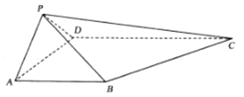
【題目】如圖所示,在四棱錐![]() 中,
中, ![]() ,底面為梯形,
,底面為梯形, ![]() 且
且![]() 平面
平面![]() .
.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)當(dāng)異面直線![]() 與
與![]() 所成角為
所成角為![]() 時,求四棱錐
時,求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求證:平面![]()
![]() 平面
平面![]() ;
;
(2)設(shè)![]() 為
為![]() 上的一點,滿足
上的一點,滿足![]() ,若直線
,若直線![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知雞的產(chǎn)蛋量與雞舍的溫度有關(guān),為了確定下一個時段雞舍的控制溫度,某企業(yè)需要了解雞舍的溫度![]() (單位:℃),對某種雞的時段產(chǎn)蛋量
(單位:℃),對某種雞的時段產(chǎn)蛋量![]() (單位:
(單位: ![]() )和時段投入成本
)和時段投入成本![]() (單位:萬元)的影響,為此,該企業(yè)收集了7個雞舍的時段控制溫度
(單位:萬元)的影響,為此,該企業(yè)收集了7個雞舍的時段控制溫度![]() 和產(chǎn)蛋量
和產(chǎn)蛋量![]() 的數(shù)據(jù),對數(shù)據(jù)初步處理后得到了如圖所示的散點圖和表中的統(tǒng)計量的值.
的數(shù)據(jù),對數(shù)據(jù)初步處理后得到了如圖所示的散點圖和表中的統(tǒng)計量的值.

|
|
|
|
|
|
|
17.40 | 82.30 | 3.6 | 140 | 9.7 | 2935.1 | 35.0 |
其中![]() .
.
(1)根據(jù)散點圖判斷, ![]() 與
與![]() 哪一個更適宜作為該種雞的時段產(chǎn)蛋量
哪一個更適宜作為該種雞的時段產(chǎn)蛋量![]() 關(guān)于雞舍時段控制溫度
關(guān)于雞舍時段控制溫度![]() 的回歸方程類型?(給判斷即可,不必說明理由)
的回歸方程類型?(給判斷即可,不必說明理由)
(2)若用![]() 作為回歸方程模型,根據(jù)表中數(shù)據(jù),建立
作為回歸方程模型,根據(jù)表中數(shù)據(jù),建立![]() 關(guān)于
關(guān)于![]() 的回歸方程;
的回歸方程;
(3)已知時段投入成本![]() 與
與![]() 的關(guān)系為
的關(guān)系為![]() ,當(dāng)時段控制溫度為28℃時,雞的時段產(chǎn)蛋量及時段投入成本的預(yù)報值分別是多少?
,當(dāng)時段控制溫度為28℃時,雞的時段產(chǎn)蛋量及時段投入成本的預(yù)報值分別是多少?
附:①對于一組具有有線性相關(guān)關(guān)系的數(shù)據(jù)![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為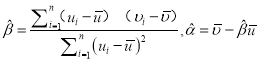
②
|
|
|
|
|
0.08 | 0.47 | 2.72 | 20.09 | 1096.63 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com