
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,
,![]() 是橢圓
是橢圓![]() 上一點,
上一點,![]() 軸,
軸,![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,
,![]() 為坐標原點,且
為坐標原點,且![]() ,求
,求![]() 面積的最大值.
面積的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)設橢圓![]() 的焦距為
的焦距為![]() ,可得出點
,可得出點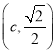 在橢圓
在橢圓![]() 上,將這個點的坐標代入橢圓
上,將這個點的坐標代入橢圓![]() 的方程可得出
的方程可得出![]() ,結合
,結合![]() 可求出
可求出![]() 的值,從而可得出橢圓
的值,從而可得出橢圓![]() 的標準方程;
的標準方程;
(2)分直線![]() 的斜率不存在與存在兩種情況討論,在
的斜率不存在與存在兩種情況討論,在![]() 軸時,可得出
軸時,可得出![]() ,從而求出
,從而求出![]() 的面積;在直線
的面積;在直線![]() 斜率存在時,設直線
斜率存在時,設直線![]() 的方程為
的方程為![]() ,設點
,設點![]() 、
、![]() ,將直線
,將直線![]() 的方程與橢圓方程聯立,利用韋達定理結合
的方程與橢圓方程聯立,利用韋達定理結合![]() ,得出
,得出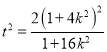 ,計算出
,計算出![]() 與
與![]() 的高,可得出
的高,可得出![]() 面積的表達式,然后可利用二次函數的基本性質求出
面積的表達式,然后可利用二次函數的基本性質求出![]() 面積的最大值.
面積的最大值.
(1)設橢圓![]() 的焦距為
的焦距為![]() ,由題知,點
,由題知,點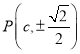 ,
,![]() ,
,
則有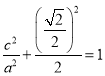 ,
,![]() ,又
,又![]() ,
,![]() ,
,![]() ,
,
因此,橢圓![]() 的標準方程為
的標準方程為![]() ;
;
(2)當![]() 軸時,
軸時,![]() 位于
位于![]() 軸上,且
軸上,且![]() ,
,
由![]() 可得
可得![]() ,此時
,此時![]() ;
;
當![]() 不垂直
不垂直![]() 軸時,設直線
軸時,設直線![]() 的方程為
的方程為![]() ,與橢圓交于
,與橢圓交于![]() ,
,![]() ,
,
由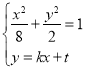 ,得
,得![]() .
.
![]() ,
,![]() ,從而
,從而![]()
已知![]() ,可得
,可得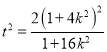 .
.
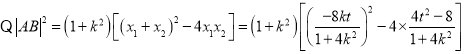
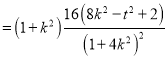 .
.
設![]() 到直線
到直線![]() 的距離為
的距離為![]() ,則
,則![]() ,
,
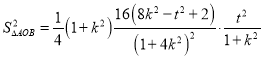 .
.
將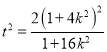 代入化簡得
代入化簡得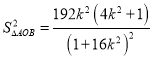 .
.
令![]() ,
,
則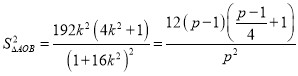
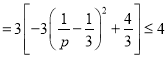 .
.
當且僅當![]() 時取等號,此時
時取等號,此時![]() 的面積最大,最大值為
的面積最大,最大值為![]() .
.
綜上:![]() 的面積最大,最大值為
的面積最大,最大值為![]() .
.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:
【題目】已知中心在原點![]() ,焦點在
,焦點在![]() 軸上,離心率為
軸上,離心率為![]() 的橢圓過點
的橢圓過點![]()

(1)求橢圓的方程;
(2)設不過原點![]() 的直線
的直線![]() 與該橢圓交于
與該橢圓交于![]() 兩點,滿足直線
兩點,滿足直線![]() 的斜率依次成等比數列,求
的斜率依次成等比數列,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知變量![]() 、
、![]() 之間的線性回歸方程為
之間的線性回歸方程為![]() ,且變量
,且變量![]() 、
、![]() 之間的一-組相關數據如下表所示,則下列說法錯誤的是( )
之間的一-組相關數據如下表所示,則下列說法錯誤的是( )
|
|
|
|
|
|
|
|
|
|
A.可以預測,當![]() 時,
時,![]() B.
B.![]()
C.變量![]()
![]() 之間呈負相關關系D.該回歸直線必過點
之間呈負相關關系D.該回歸直線必過點![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年,教育部發文確定新高考改革正式啟動,湖南、廣東、湖北等8省市開始實行新高考制度,從2018年下學期的高一年級學生開始實行.為了適應新高考改革,某校組織了一次新高考質量測評,在成績統計分析中,高二某班的數學成績的莖葉圖和頻率分布直方圖因故都受到不同程度的損壞,但可見部分如下,據此解答如下問題:
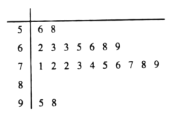
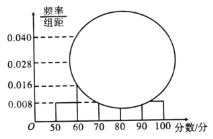
(1)求該班數學成績在![]() 的頻率及全班人數;
的頻率及全班人數;
(2)根據頻率分布直方圖估計該班這次測評的數學平均分;
(3)若規定![]() 分及其以上為優秀,現從該班分數在
分及其以上為優秀,現從該班分數在![]() 分及其以上的試卷中任取
分及其以上的試卷中任取![]() 份分析學生得分情況,求在抽取的
份分析學生得分情況,求在抽取的![]() 份試卷中至少有
份試卷中至少有![]() 份優秀的概率.
份優秀的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圓周上有1994個點,將它們染成若干種不同的顏色,且每種顏色的點數各不相同.今在每種顏色的點集中各取一個點,組成頂點顏色各不相同的圓內接多邊形,為了要使這樣的多邊形個數最多,應將1994個點染成多少種不同的顏色?且每種顏色的點集各含有多少個點?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年某地遭遇嚴重干旱,某鄉計劃向上級申請支援,為上報需水量,鄉長事先抽樣調查100戶村民的月均用水量,得到這100戶村民月均用水量(單位:t)的頻率分布表如下:
月均用水量分組 | 頻數 | 頻率 |
| 12 | |
| ||
| 40 | |
| 0.18 | |
| 6 | |
合計 | 100 | 1.00 |
(1)請完成該頻率分布表,并畫出相對應的頻率分布直方圖.
(2)樣本的中位數是多少?
(3)已知上級將按每戶月均用水量向該鄉調水,若該鄉共有1200戶,請估計上級支援該鄉的月調水量是多少噸.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com