
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,若橢圓經過點
,若橢圓經過點![]() ,且
,且![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設斜率為![]() 的直線
的直線![]() 與以原點為圓心,半徑為
與以原點為圓心,半徑為![]() 的圓交于
的圓交于![]() ,
,![]() 兩點,與橢圓
兩點,與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,當
,當![]() 取得最小值時,求直線
取得最小值時,求直線![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 最小值
最小值![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
【解析】試題分析:(1)由三角形的面積![]() ,即可求得c=2,將點
,即可求得c=2,將點![]() 代入橢圓方程,由橢圓的性質a2=b2+c2,即可求得a和b的值,求得橢圓方程;
代入橢圓方程,由橢圓的性質a2=b2+c2,即可求得a和b的值,求得橢圓方程;
(2)直線![]() 的方程為
的方程為![]() ,則原點到直線
,則原點到直線![]() 的距離
的距離![]() ,由弦長公式可得
,由弦長公式可得![]() .將
.將![]() 代入橢圓方程
代入橢圓方程![]() ,得
,得![]() ,得
,得![]() .可得
.可得![]() .可得所求結論.
.可得所求結論.
試題解析:(1)由![]() 的面積可得
的面積可得![]() ,即
,即![]() ,∴
,∴![]() .①
.①
又橢圓![]() 過點
過點![]() ,∴
,∴![]() .②
.②
由①②解得![]() ,
,![]() ,故橢圓
,故橢圓![]() 的標準方程為
的標準方程為![]() .
.
(2)設直線![]() 的方程為
的方程為![]() ,則原點到直線
,則原點到直線![]() 的距離
的距離![]() ,
,
由弦長公式可得![]() .
.
將![]() 代入橢圓方程
代入橢圓方程![]() ,得
,得![]() ,
,
由判別式![]() ,解得
,解得![]() .
.
由直線和圓相交的條件可得![]() ,即
,即![]() ,也即
,也即![]() ,
,
綜上可得![]() 的取值范圍是
的取值范圍是![]() .
.
設![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
由弦長公式,得![]() .
.
由![]() ,得
,得![]() .
.
∵![]() ,∴
,∴![]() ,則當
,則當![]() 時,
時,![]() 取得最小值
取得最小值![]() ,此時直線
,此時直線![]() 的方程為
的方程為![]() .
.
點睛:本題主要考查直線與圓錐曲線位置關系,所使用方法為韋達定理法:因直線的方程是一次的,圓錐曲線的方程是二次的,故直線與圓錐曲線的問題常轉化為方程組關系問題,最終轉化為一元二次方程問題,故用韋達定理及判別式是解決圓錐曲線問題的重點方法之一,尤其是弦中點問題,弦長問題,可用韋達定理直接解決,但應注意不要忽視判別式的作用.


科目:高中數學 來源: 題型:
【題目】橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,過其右焦點
,過其右焦點![]() 與長軸垂直的直線與橢圓在第一象限相交于點
與長軸垂直的直線與橢圓在第一象限相交于點![]() ,
, ![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設橢圓![]() 的左頂點為
的左頂點為![]() ,右頂點為
,右頂點為![]() ,點
,點![]() 是橢圓上的動點,且點
是橢圓上的動點,且點![]() 與點
與點![]() ,
, ![]() 不重合,直線
不重合,直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,直線
,直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,求證:以線段
,求證:以線段![]() 為直徑的圓恒過定點.
為直徑的圓恒過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
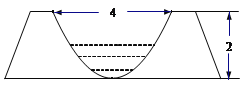
【題目】為響應新農村建設,某村計劃對現有舊水渠進行改造,已知舊水渠的橫斷面是一段拋物線弧,頂點為水渠最底端(如圖),渠寬為4m,渠深為2m.
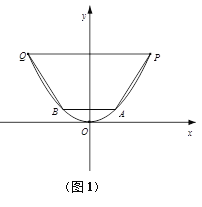
(1)考慮到農村耕地面積的減少,為節約水資源,要減少水渠的過水量,在原水渠內填土,使其成為橫斷面為等腰梯形的新水渠(如圖(1)建立平面直角坐標系),新水渠底面與地面平行(不改變渠寬),問新水渠底寬為多少時,所填土的土方量最少?
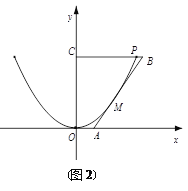
(2)考慮到新建果園的灌溉需求,要增大水渠的過水量,現把舊水渠改挖(不能填土)成橫斷面為等腰梯形的新水渠(如圖(2)建立平面直角坐標系),使水渠的底面與地面平行(不改變渠深),要使所挖土的土方量最少,請你設計水渠改挖后的底寬,并求出這個底寬.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著我國經濟的快速發展,民用汽車的保有量也迅速增長.機動車保有量的發展影響到環境質量、交通安全、道路建設等諸多方面.在我國,尤其是大中型城市,機動車已成為城市空氣污染的重要來源.因此,合理預測機動車保有量是未來進行機動車污染防治規劃、道路發展規劃等的重要前提.從2012年到2016年,根據“云南省某市國民經濟和社會發展統計公報”中公布的數據,該市機動車保有量數據如表所示.
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代碼 | 1 | 2 | 3 | 4 | 5 |
機動車保有量 | 169 | 181 | 196 | 215 | 230 |
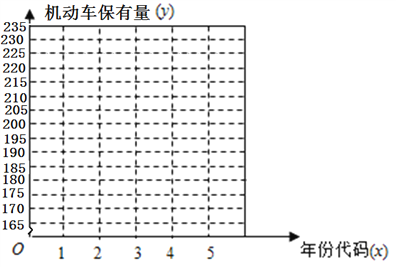
(1)在圖所給的坐標系中作出數據對應的散點圖;
(2)建立機動車保有量![]() 關于年份代碼
關于年份代碼![]() 的回歸方程;
的回歸方程;
(3)按照當前的變化趨勢,預測2017年該市機動車保有量.
附注:回歸直線方程![]() 中的斜率和截距的最小二乘估計公式分別為:
中的斜率和截距的最小二乘估計公式分別為:
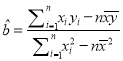 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位最近組織了一次健身活動,活動分為登山組和游泳組,且每個職工至多參加其中一組.在參加活動的職工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山組的職工占參加活動總人數的![]() ,且該組中青年人占50%,中年人占40%,老年人占10%.為了了解各組不同年齡層次的職工對本次活動的滿意程度,現用分層抽樣的方法從參加活動的全體職工中抽取一個容量為200的樣本.試確定:
,且該組中青年人占50%,中年人占40%,老年人占10%.為了了解各組不同年齡層次的職工對本次活動的滿意程度,現用分層抽樣的方法從參加活動的全體職工中抽取一個容量為200的樣本.試確定:
(1)游泳組中,青年人、中年人、老年人分別所占的比例;
(2)游泳組中,青年人、中年人、老年人分別應抽取的人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com