
【題目】已知橢圓E: ![]() (a>b>0)的左焦點(diǎn)F1與拋物線(xiàn)y2=﹣4x的焦點(diǎn)重合,橢圓E的離心率為
(a>b>0)的左焦點(diǎn)F1與拋物線(xiàn)y2=﹣4x的焦點(diǎn)重合,橢圓E的離心率為 ![]() ,過(guò)點(diǎn)M (m,0)(m>
,過(guò)點(diǎn)M (m,0)(m> ![]() )作斜率不為0的直線(xiàn)l,交橢圓E于A,B兩點(diǎn),點(diǎn)P(
)作斜率不為0的直線(xiàn)l,交橢圓E于A,B兩點(diǎn),點(diǎn)P( ![]() ,0),且
,0),且 ![]() 為定值.
為定值.
(Ⅰ)求橢圓E的方程;
(Ⅱ)求△OAB面積的最大值.
【答案】解:(Ⅰ)設(shè)F1(﹣c,0),
∵拋物線(xiàn)y2=﹣4x的焦點(diǎn)坐標(biāo)為(﹣1,0),且橢圓E的左焦點(diǎn)F與拋物線(xiàn)y2=﹣4x的焦點(diǎn)重合,∴c=1,
又橢圓E的離心率為 ![]() ,得a=
,得a= ![]() ,于是有b2=a2﹣c2=1.
,于是有b2=a2﹣c2=1.
故橢圓Γ的標(biāo)準(zhǔn)方程為: ![]() .
.
(Ⅱ)設(shè)A(x1 , y1),B(x2 , y2),直線(xiàn)l的方程為:x=ty+m,
由 ![]() 整理得(t2+2)y2+2tmy+m2﹣2=0
整理得(t2+2)y2+2tmy+m2﹣2=0![]() ,
,![]() ,
, ![]() =
= ![]()
=(t2+1)y1y2+(tm﹣ ![]() t)(y1+y2)+m2﹣
t)(y1+y2)+m2﹣ ![]() =
= ![]() .
.
要使 ![]() 為定值,則
為定值,則 ![]() ,解得m=1或m=
,解得m=1或m= ![]() (舍)
(舍)
當(dāng)m=1時(shí),|AB|= ![]() |y1﹣y2|=
|y1﹣y2|= ![]() ,
,
點(diǎn)O到直線(xiàn)AB的距離d= ![]() ,
,
△OAB面積s= ![]() =
= ![]() .
.
∴當(dāng)t=0,△OAB面積的最大值為 ![]()
【解析】(Ⅰ)由拋物線(xiàn)方程求出拋物線(xiàn)的焦點(diǎn)坐標(biāo),即橢圓左焦點(diǎn)坐標(biāo),結(jié)合橢圓離心率可得長(zhǎng)半軸長(zhǎng),再由b2=a2﹣c2求出短半軸,則橢圓E的標(biāo)準(zhǔn)方程可求;(Ⅱ)設(shè)A(x1 , y1),B(x2 , y2),直線(xiàn)l的方程為:x=ty+m,由 ![]() 整理得(t2+2)y2+2tmy+m2﹣2=0由
整理得(t2+2)y2+2tmy+m2﹣2=0由 ![]() 為定值,解得m,|AB|=
為定值,解得m,|AB|= ![]() |y1﹣y2|=
|y1﹣y2|= ![]() ,點(diǎn)O到直線(xiàn)AB的距離d=
,點(diǎn)O到直線(xiàn)AB的距離d= ![]() ,△OAB面積s=
,△OAB面積s= ![]() 即可求得最值
即可求得最值
【考點(diǎn)精析】利用橢圓的標(biāo)準(zhǔn)方程對(duì)題目進(jìn)行判斷即可得到答案,需要熟知橢圓標(biāo)準(zhǔn)方程焦點(diǎn)在x軸:![]() ,焦點(diǎn)在y軸:
,焦點(diǎn)在y軸:![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四邊形ABCD中,AB=AD=CD=1,BD= ![]() ,BD⊥CD.將四邊形ABCD沿對(duì)角線(xiàn)BD折成四面體A′﹣BCD,使平面A′BD⊥平面BCD,則下列結(jié)論正確的是( )
,BD⊥CD.將四邊形ABCD沿對(duì)角線(xiàn)BD折成四面體A′﹣BCD,使平面A′BD⊥平面BCD,則下列結(jié)論正確的是( ) 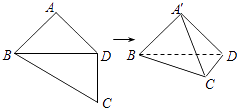
A.A′C⊥BD
B.∠BA′C=90°
C.CA′與平面A′BD所成的角為30°
D.四面體A′﹣BCD的體積為 ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某地區(qū)上年度電價(jià)為![]() 元/kWh,年用電量為
元/kWh,年用電量為![]() kWh.本年度計(jì)劃將電價(jià)降低到0.55元/ kWh到0.75元/ kWh之間,而用戶(hù)期望電價(jià)為0.40元/ kWh.經(jīng)測(cè)算,下調(diào)電價(jià)后新增用電量與實(shí)際電價(jià)與用戶(hù)的期望電價(jià)的差成反比(比例系數(shù)為
kWh.本年度計(jì)劃將電價(jià)降低到0.55元/ kWh到0.75元/ kWh之間,而用戶(hù)期望電價(jià)為0.40元/ kWh.經(jīng)測(cè)算,下調(diào)電價(jià)后新增用電量與實(shí)際電價(jià)與用戶(hù)的期望電價(jià)的差成反比(比例系數(shù)為![]() ),該地區(qū)電力的成本價(jià)為0.30元/ kWh.
),該地區(qū)電力的成本價(jià)為0.30元/ kWh.
(1)寫(xiě)出本年度電價(jià)下調(diào)后,電力部門(mén)的收益![]() 與實(shí)際電價(jià)
與實(shí)際電價(jià)![]() 之間的函數(shù)關(guān)系式;
之間的函數(shù)關(guān)系式;
(2)設(shè)![]() =
=![]() ,當(dāng)電價(jià)最低定為多少時(shí)仍可保證電力部門(mén)的收益比上一年至少增長(zhǎng)20%?(注:收益=實(shí)際電量×(實(shí)際電價(jià)-成本價(jià)))
,當(dāng)電價(jià)最低定為多少時(shí)仍可保證電力部門(mén)的收益比上一年至少增長(zhǎng)20%?(注:收益=實(shí)際電量×(實(shí)際電價(jià)-成本價(jià)))
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列四個(gè)命題:
①命題“若a=0,則ab=0”的否命題是“若a=0,則ab≠0”;
②已知命題p:x∈R,x2+x+1<0,則![]() p:x∈R,x2+x+1≥0;
p:x∈R,x2+x+1≥0;
③若命題“![]() p”與命題“p或q”都是真命題,則命題q一定是真命題;
p”與命題“p或q”都是真命題,則命題q一定是真命題;
④命題“若0<a<1,則loga(a+1)<lo![]() .
.
其中正確命題的序號(hào)是_____.(把所有正確的命題序號(hào)都填上)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列四個(gè)結(jié)論:
①命題“若a=0,則ab=0”的否命題是“若a=0,則ab≠0”;
②已知命題p:x∈R,x2+6x+11<0,則![]() p:x∈R,x2+6x+11≥0;
p:x∈R,x2+6x+11≥0;
③若命題“![]() p”與命題“p或q”都是真命題,則命題q一定是真命題;
p”與命題“p或q”都是真命題,則命題q一定是真命題;
④命題“若0<a<1,則loga(a+1)<log![]()
其中正確結(jié)論的序號(hào)是_____.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系xOy中,直線(xiàn)l的參數(shù)方程為  (t為參數(shù)),在以原點(diǎn)O為極點(diǎn),x軸正半軸為極軸的極坐標(biāo)系中,圓C的方程為ρ=6sinθ.
(t為參數(shù)),在以原點(diǎn)O為極點(diǎn),x軸正半軸為極軸的極坐標(biāo)系中,圓C的方程為ρ=6sinθ.
(Ⅰ)寫(xiě)出直線(xiàn)l的普通方程和圓C的直角坐標(biāo)方程;
(Ⅱ)設(shè)點(diǎn)P(4,3),直線(xiàn)l與圓C相交于A,B兩點(diǎn),求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】我國(guó)南宋時(shí)期的著名數(shù)學(xué)家秦九韶在他的著作《數(shù)學(xué)九章》中提出了秦九韶算法來(lái)計(jì)算多項(xiàng)式的值,在執(zhí)行如圖算法的程序框圖時(shí),若輸入的n=5,x=2,則輸出V的值為( ) 
A.15
B.31
C.63
D.127
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某教師調(diào)查了![]() 名高三學(xué)生購(gòu)買(mǎi)的數(shù)學(xué)課外輔導(dǎo)書(shū)的數(shù)量,將統(tǒng)計(jì)數(shù)據(jù)制成如下表格:
名高三學(xué)生購(gòu)買(mǎi)的數(shù)學(xué)課外輔導(dǎo)書(shū)的數(shù)量,將統(tǒng)計(jì)數(shù)據(jù)制成如下表格:
男生 | 女生 | 總計(jì) | |
購(gòu)買(mǎi)數(shù)學(xué)課外輔導(dǎo)書(shū)超過(guò) |
|
|
|
購(gòu)買(mǎi)數(shù)學(xué)課外輔導(dǎo)書(shū)不超過(guò) |
|
|
|
總計(jì) |
|
|
|
(Ⅰ)根據(jù)表格中的數(shù)據(jù),是否有![]() 的把握認(rèn)為購(gòu)買(mǎi)數(shù)學(xué)課外輔導(dǎo)書(shū)的數(shù)量與性別相關(guān);
的把握認(rèn)為購(gòu)買(mǎi)數(shù)學(xué)課外輔導(dǎo)書(shū)的數(shù)量與性別相關(guān);
(Ⅱ)從購(gòu)買(mǎi)數(shù)學(xué)課外輔導(dǎo)書(shū)不超過(guò)![]() 本的學(xué)生中,按照性別分層抽樣抽取
本的學(xué)生中,按照性別分層抽樣抽取![]() 人,再?gòu)倪@
人,再?gòu)倪@![]() 人中隨機(jī)抽取
人中隨機(jī)抽取![]() 人詢(xún)問(wèn)購(gòu)買(mǎi)原因,求恰有
人詢(xún)問(wèn)購(gòu)買(mǎi)原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() ,則下列結(jié)論正確的是( )
,則下列結(jié)論正確的是( )
A.當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 在
在![]() 上有最小值;
上有最小值;
B.當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 在
在![]() 上有最小值;
上有最小值;
C.對(duì)任意的實(shí)數(shù)![]() ,函數(shù)
,函數(shù)![]() 的圖象關(guān)于點(diǎn)
的圖象關(guān)于點(diǎn)![]() 對(duì)稱(chēng);
對(duì)稱(chēng);
D.方程![]() 可能有三個(gè)實(shí)數(shù)根.
可能有三個(gè)實(shí)數(shù)根.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com