
【題目】已知函數 ![]() .
.
(1)當m=1時,求證:對x∈[0,+∞)時,f(x)≥0;
(2)當m≤1時,討論函數f(x)零點的個數.
【答案】
(1)證明:當m=1時, ![]() ,則f'(x)=ex﹣x﹣1,
,則f'(x)=ex﹣x﹣1,
令g(x)=ex﹣x﹣1,則g'(x)=ex﹣1,當x≥0時,ex﹣1≥0,即g'(x)≥0,
所以函數f'(x)=ex﹣x﹣1在[0,+∞)上為增函數,
即當x≥0時,f'(x)≥f'(0),所以當x≥0時,f'(x)≥0恒成立,
所以函數 ![]() ,在[0,+∞)上為增函數,又因為f(0)=0,
,在[0,+∞)上為增函數,又因為f(0)=0,
所以當m=1時,對x∈[0,+∞),f(x)≥0恒成立
(2)解:由(1)知,當x≤0時,ex﹣1≤0,所以g'(x)≤0,所以函數f'(x)=ex﹣x﹣1的減區間為(﹣∞,0],增區間為[0,+∞).所以f'(x)min=f'(0)=0,所以對x∈R,f'(x)≥0,即ex≥x+1.
①當x≥﹣1時,x+1≥0,又m≤1,∴m(x+1)≤x+1,∴ex﹣m(x+1)≥ex﹣(x+1)≥0,即f'(x)≥0,所以當x≥﹣1時,函數f(x)為增函數,又f(0)=0,所以當x>0時,f(x)>0,當﹣1≤x<0時,f(x)<0,所以函數f(x)在區間[﹣1,+∞)上有且僅有一個零點,且為0.
②當x<﹣1時,(ⅰ)當0≤m≤1時,﹣m(x+1)≥0,ex>0,所以f'(x)=ex﹣m(x+1)>0,
所以函數f(x)在(﹣∞,﹣1)上遞增,所以f(x)<f(﹣1),且 ![]() ,
,
故0≤m≤1時,函數y=f(x)在區間(﹣∞,﹣1)上無零點.
(ⅱ)當m<0時,f'(x)=ex﹣mx﹣m,令h(x)=ex﹣mx﹣m,則h'(x)=ex﹣m>0,
所以函數f'(x)=ex﹣mx﹣m在(﹣∞,﹣1)上單調遞增,f'(﹣1)=e﹣1>0,
當 ![]() 時,
時, ![]() ,又曲線f'(x)在區間
,又曲線f'(x)在區間 ![]() 上不間斷,
上不間斷,
所以x0∈ ![]() ,使f'(x0)=0,
,使f'(x0)=0,
故當x∈(x0,﹣1)時,0=f'(x0)<f'(x)<f'(﹣1)=e﹣1,
當x∈(﹣∞,x0)時,f'(x)<f'(x0)=0,
所以函數 ![]() 的減區間為(﹣∞,x0),增區間為(x0,﹣1),
的減區間為(﹣∞,x0),增區間為(x0,﹣1),
又 ![]() ,所以對x∈[x0,﹣1),f(x)<0,
,所以對x∈[x0,﹣1),f(x)<0,
又當 ![]() 時,
時, ![]() ,∴f(x)>0,
,∴f(x)>0,
又f(x0)<0,曲線 ![]() 在區間
在區間 ![]() 上不間斷.
上不間斷.
所以x1∈(﹣∞,x0),且唯一實數x1,使得f(x1)=0,
綜上,當0≤m≤1時,函數y=f(x)有且僅有一個零點;當m<0時,函數y=f(x)有個兩零點
【解析】(1)當m=1時, ![]() ,則f'(x)=ex﹣x﹣1,令g(x)=ex﹣x﹣1,利用導數研究其單調性極值與最值,可得函數f'(x)=ex﹣x﹣1在[0,+∞)上為增函數,即當x≥0時,f'(x)≥f'(0)=0,可得函數f(x)在(0,+∞)上為增函數,即可證明.(2)由(1)知,當x≤0時,ex﹣1≤0,所以g'(x)≤0,可得ex≥x+1.①當x≥﹣1時,x+1≥0,又m≤1,m(x+1)≤x+1,可得ex﹣m(x+1)≥0,即f'(x)≥0,可得:函數f(x)在區間[﹣1,+∞)上有且僅有一個零點,且為0.②當x<﹣1時,(ⅰ)當0≤m≤1時,﹣m(x+1)≥0,ex>0,可得f'(x)=ex﹣m(x+1)>0,函數f(x)在(﹣∞,﹣1)上遞增,函數y=f(x)在區間(﹣∞,﹣1)上無零點. (ⅱ)當m<0時,f'(x)=ex﹣mx﹣m,令h(x)=ex﹣mx﹣m,則h'(x)>0,函數f'(x)=ex﹣mx﹣m在(﹣∞,﹣1)上單調遞增,f'(﹣1)=e﹣1>0,可得函數存在兩個零點.
,則f'(x)=ex﹣x﹣1,令g(x)=ex﹣x﹣1,利用導數研究其單調性極值與最值,可得函數f'(x)=ex﹣x﹣1在[0,+∞)上為增函數,即當x≥0時,f'(x)≥f'(0)=0,可得函數f(x)在(0,+∞)上為增函數,即可證明.(2)由(1)知,當x≤0時,ex﹣1≤0,所以g'(x)≤0,可得ex≥x+1.①當x≥﹣1時,x+1≥0,又m≤1,m(x+1)≤x+1,可得ex﹣m(x+1)≥0,即f'(x)≥0,可得:函數f(x)在區間[﹣1,+∞)上有且僅有一個零點,且為0.②當x<﹣1時,(ⅰ)當0≤m≤1時,﹣m(x+1)≥0,ex>0,可得f'(x)=ex﹣m(x+1)>0,函數f(x)在(﹣∞,﹣1)上遞增,函數y=f(x)在區間(﹣∞,﹣1)上無零點. (ⅱ)當m<0時,f'(x)=ex﹣mx﹣m,令h(x)=ex﹣mx﹣m,則h'(x)>0,函數f'(x)=ex﹣mx﹣m在(﹣∞,﹣1)上單調遞增,f'(﹣1)=e﹣1>0,可得函數存在兩個零點.


 字詞句段篇系列答案
字詞句段篇系列答案科目:高中數學 來源: 題型:
【題目】隨著網絡營銷和電子商務的興起,人們的購物方式更具多樣化,某調查機構隨機抽取10名購物者進行采訪,5名男性購物者中有3名傾向于選擇網購,2名傾向于選擇實體店,5名女性購物者中有2名傾向于選擇網購,3名傾向于選擇實體店.
(1)若從10名購物者中隨機抽取2名,其中男、女各一名,求至少1名傾向于選擇實體店的概率;
(2)若從這10名購物者中隨機抽取3名,設X表示抽到傾向于選擇網購的男性購物者的人數,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正△ABC三個頂點都在半徑為2的球面上,球心O到平面ABC的距離為1,點E是線段AB的中點,過點E作球O的截面,則截面面積的最小值是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著生活水平的提高,人們對空氣質量的要求越來越高,某機構為了解公眾對“車輛限行”的態度,隨機抽查50人,并將調查情況進行整理后制成如表:
年齡(歲) | [15,25) | [25,35) | [35,45) | [45,55) | [55,60) |
頻數 | 10 | 10 | 10 | 10 | 10 |
贊成人數 | 3 | 5 | 6 | 7 | 9 |
(1)世界聯合國衛生組織規定:[15,45)歲為青年,(45,60)為中年,根據以上統計數據填寫以下2×2列聯表:
青年人 | 中年人 | 合計 | |
不贊成 |
|
|
|
贊成 |
|
|
|
合計 |
|
|
|
(2)判斷能否在犯錯誤的概率不超過0.05的前提下,認為贊成“車柄限行”與年齡有關? 附: ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
獨立檢驗臨界值表:
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
(3)若從年齡[15,25),[25,35)的被調查中各隨機選取1人進行調查,設選中的兩人中持不贊成“車輛限行”態度的人員為ξ,求隨機變量ξ的分布列和數學期望Eξ.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】參與舒城中學數學選修課的同學對某公司的一種產品銷量與價格進行了統計,得到如下數據和散點圖.
定價x(元/千克) | 10 | 20 | 30 | 40 | 50 | 60 |
年銷量y(千克) | 1150 | 643 | 424 | 262 | 165 | 86 |
z=2 ln y | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

參考數據:
![]() ,
,
![]() .
.
(1)根據散點圖判斷y與x,z與x哪一對具有較強的線性相關性(給出判斷即可,不必說明理由)?
(2)根據(1)的判斷結果及數據,建立y關于x的回歸方程(方程中的系數均保留兩位有效數字).
(3)當定價為150元/千克時,試估計年銷量.
附:對于一組數據(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),其回歸直線![]() x+
x+![]() 的斜率和截距的最
的斜率和截距的最
小二乘估計分別為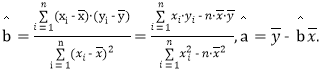
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】德國著名數學家狄利克雷在數學領域成就顯著,以其名命名的函數f(x)= ![]() ,稱為狄利克雷函數,則關于函數f(x)有以下四個命題: ①f(f(x))=1;
,稱為狄利克雷函數,則關于函數f(x)有以下四個命題: ①f(f(x))=1;
②函數f(x)是偶函數;
③任意一個非零有理數T,f(x+T)=f(x)對任意x∈R恒成立;
④存在三個點A(x1 , f(x1)),B(x2 , f(x2)),C(x3 , f(x3)),使得△ABC為等邊三角形.
其中真命題的個數是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=|x﹣4|,g(x)=|2x+1|.
(1)解不等式f(x)<g(x);
(2)若2f(x)+g(x)>ax對任意的實數x恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣1|﹣|x+2|. (Ⅰ)求不等式﹣2<f(x)<0的解集A;
(Ⅱ)若m,n∈A,證明:|1﹣4mn|>2|m﹣n|.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com