
【題目】圖,從甲地到丙地要經過兩個十字路口(十字路口![]() 與十字路口
與十字路口![]() ),從乙地到丙地也要經過兩個十字路口(十字路口
),從乙地到丙地也要經過兩個十字路口(十字路口![]() 與十字路口
與十字路口![]() ),設各路口信號燈工作相互獨立,且在
),設各路口信號燈工作相互獨立,且在![]() ,
,![]() ,
,![]() ,
,![]() 路口遇到紅燈的概率分別為
路口遇到紅燈的概率分別為![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求一輛車從乙地到丙地至少遇到一個紅燈的概率;
(2)若小方駕駛一輛車從甲地出發,小張駕駛一輛車從乙地出發,他們相約在丙地見面,記![]() 表示這兩人見面之前車輛行駛路上遇到的紅燈的總個數,求
表示這兩人見面之前車輛行駛路上遇到的紅燈的總個數,求![]() 的分布列及數學期望.
的分布列及數學期望.
 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案科目:高中數學 來源: 題型:
【題目】已知直線l的參數方程為 ![]() (t為參數),圓C的參數方程為
(t為參數),圓C的參數方程為 ![]() (θ為常數).
(θ為常數).
(1)求直線l和圓C的普通方程;
(2)若直線l與圓C有公共點,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中正確的有______
①平均數不受少數幾個極端值的影響,中位數受樣本中的每一個數據影響;
②拋擲兩枚硬幣,出現“兩枚都是正面朝上”、“兩枚都是反面朝上”、“恰好一枚硬幣正面朝上”的概率一樣大
③用樣本的頻率分布估計總體分布的過程中,樣本容量越大,估計越準確.
④向一個圓面內隨機地投一個點,如果該點落在圓內任意一點都是等可能的,則該隨機試驗的數學模型是古典概型.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C的圓心在x軸正半軸上,半徑為5,且與直線![]() 相切.
相切.
(1)求圓C的方程;
(2)設點![]() ,過點
,過點![]() 作直線
作直線![]() 與圓C交于
與圓C交于![]() 兩點,若
兩點,若![]() ,求直線
,求直線![]() 的方程;
的方程;
(3)設P是直線![]() 上的點,過P點作圓C的切線
上的點,過P點作圓C的切線![]() ,切點為
,切點為![]() 求證:經過
求證:經過![]() 三點的圓必過定點,并求出所有定點的坐標.
三點的圓必過定點,并求出所有定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩個不相等的非零向量 ![]() ,
, ![]() ,兩組向量
,兩組向量 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 和
和 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 均由2個
均由2個 ![]() 和3個
和3個 ![]() 排列而成,記S=
排列而成,記S= ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() ,Smin表示S所有可能取值中的最小值.則下列命題正確的是(寫出所有正確命題的編號).
,Smin表示S所有可能取值中的最小值.則下列命題正確的是(寫出所有正確命題的編號).
①S有5個不同的值;
②若 ![]() ⊥
⊥ ![]() ,則Smin與|
,則Smin與| |無關;
③若 ![]() ∥
∥ ![]() ,則Smin與|
,則Smin與| ![]() |無關;
|無關;
④若| ![]() |>4|
|>4| ![]() |,則Smin>0;
|,則Smin>0;
⑤若| ![]() |=2|
|=2| ![]() |,Smin=8|
|,Smin=8| ![]() |2 , 則
|2 , 則 ![]() 與
與 ![]() 的夾角為
的夾角為 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解學生的課外閱讀時間情況,某學校隨機抽取了50人進行統計分析,把這50人每天閱讀的時間(單位:分鐘)繪制成頻數分布表,如下表所示:
閱讀時間 |
|
|
|
|
|
|
人數 | 8 | 10 | 12 | 11 | 7 | 2 |
若把每天閱讀時間在60分鐘以上(含60分鐘)的同學稱為“閱讀達人”,根據統計結果中男女生閱讀達人的數據,制作成如圖所示的等高條形圖.
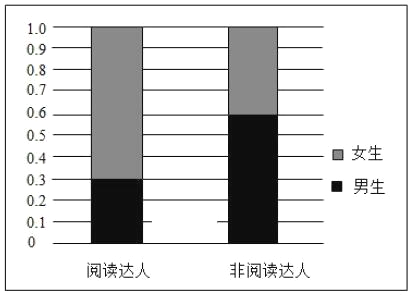
(1)根據抽樣結果估計該校學生的每天平均閱讀時間(同一組數據用該區間的終點值作為代表);
(2)根據已知條件完成下面的![]() 列聯表,并判斷是否有99%的把握認為“閱讀達人”跟性別有關?
列聯表,并判斷是否有99%的把握認為“閱讀達人”跟性別有關?
男生 | 女生 | 總計 | |
閱讀達人 | |||
非閱讀達人 | |||
總計 |
附:參考公式![]() ,其中
,其中![]() .
.
臨界值表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查觀眾對電視劇《風箏》的喜愛程度,某電視臺舉辦了一次現場調查活動.在參加此活動的甲、乙兩地大量觀眾中,各隨機抽取了8名觀眾對該電視劇評分做調查(滿分100分),被抽取的觀眾的評分結果如圖所示.

(1)從甲地抽取的8名觀眾和乙地抽取的8名觀眾中分別各選取一人,在已知兩人中至少一人評分不低于90分的條件下,求乙地被選取的觀眾評分低于90分的概率。
(2)從甲地抽取出來的8名觀眾中選取1人,從乙地抽取出來的8名觀眾中選取2人去參加代表大會,記選取的3人中評分不低于90分的人數為![]() ,求
,求![]() 的分布列與期望。
的分布列與期望。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com