Question

【題目】已知直線l的參數方程為 （t為參數），圓C的參數方程為 （θ為常數）．
（1）求直線l和圓C的普通方程；
（2）若直線l與圓C有公共點，求實數a的取值范圍．

Answer 1

【答案】
（1）解：直線l的參數方程為 ，消去t可得2x﹣y﹣2a=0；

圓C的參數方程為 ，兩式平方相加可得x2+y2=16

（2）解：圓心C（0，0），半徑r=4．

由點到直線的距離公式可得圓心C（0，0）到直線L的距離d= ．

∵直線L與圓C有公共點，∴d≤4，即 ≤4，解得﹣2 ≤a≤2

【解析】（1）消去參數，把直線與圓的參數方程化為普通方程；（2）求出圓心到直線的距離d，再根據直線l與圓C有公共點d≤r即可求出．
【考點精析】解答此題的關鍵在于理解直線的參數方程的相關知識，掌握經過點，傾斜角為的直線的參數方程可表示為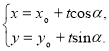（為參數），以及對圓的參數方程的理解，了解圓的參數方程可表示為．