精品国产三级电影在线观看,欧美精品一区二区三区很污很色的,欧美亚洲视频在线观看

【題目】鈍角三角形ABC的面積是，AB=1，BC= ，則AC=（）
A.5
B.
C.2
D.1

【答案】B
【解析】解：∵鈍角三角形ABC的面積是，AB=c=1，BC=a= ，
∴S= acsinB= ，即sinB= ，
當B為鈍角時，cosB=﹣ =﹣ ，
利用余弦定理得：AC2=AB2+BC2﹣2ABBCcosB=1+2+2=5，即AC= ，
當B為銳角時，cosB= = ，
利用余弦定理得：AC2=AB2+BC2﹣2ABBCcosB=1+2﹣2=1，即AC=1，
此時AB2+AC2=BC2 ，即△ABC為直角三角形，不合題意，舍去，
則AC= ．
故選：B．
【考點精析】解答此題的關鍵在于理解余弦定理的定義的相關知識，掌握余弦定理:;;．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

【題目】如圖，在直角△ABC中，AB⊥BC，D為BC邊上異于B、C的一點，以AB為直徑作⊙O，并分別交AC，AD于點E，F．

（1）證明：C，E，F，D四點共圓；
（2）若D為BC的中點，且AF=3，FD=1，求AE的長．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】函數的性質通常指函數的定義域、值域、周期性、單調性、奇偶性、對稱性等，請選擇適當的探究順序，研究函數的性質，并在此基礎上填寫下表，作出f（x）在區間[-π，2π]上的圖象．

性質	理由	結論	得分
定義域
值域
奇偶性
周期性
單調性
對稱性
作圖

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】如圖在長為10千米的河流的一側有一條觀光帶，觀光帶的前一部分為曲線段，設曲線段為函數（單位：千米）的圖象，且圖象的最高點為；觀光帶的后一部分為線段．

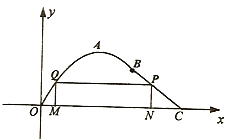
（1）求函數為曲線段的函數的解析式；

（2）若計劃在河流和觀光帶之間新建一個如圖所示的矩形綠化帶，綠化帶僅由線段構成，其中點在線段上．當長為多少時，綠化帶的總長度最長？

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數f（x）=x2（lnx+lna）（a＞0）．
（1）當a=1時，設函數g（x）= ，求函數g（x）的單調區間與極值；
（2）設f′（x）是f（x）的導函數，若 ≤1對任意的x＞0恒成立，求實數a的取值范圍；
（3）若x1 ， x2∈（，1），x1+x2＜1，求證：x1x2＜（x1+x2）4 ．