
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,且過(guò)點(diǎn)
,且過(guò)點(diǎn)![]() .
.
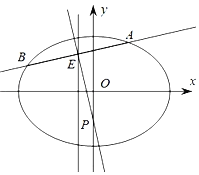
(1)求橢圓C的方程;
(2)直線l交橢圓C于不同的兩點(diǎn)A、B,且![]() 中點(diǎn)E在直線
中點(diǎn)E在直線![]() 上,線段
上,線段![]() 的垂直平分線交y軸于點(diǎn)
的垂直平分線交y軸于點(diǎn)![]() ,求m的取值范圍.
,求m的取值范圍.
【答案】(1)![]() (2)
(2)
【解析】
(1)由離心率及橢圓所過(guò)的點(diǎn)的坐標(biāo)及![]() 之間的關(guān)系求出橢圓的方程;
之間的關(guān)系求出橢圓的方程;
(2)由題意設(shè)直線![]() 的方程與橢圓聯(lián)立求出兩根之和,進(jìn)而求出中點(diǎn)的橫坐標(biāo),代入直線求出中點(diǎn)的縱坐標(biāo),進(jìn)而求出
的方程與橢圓聯(lián)立求出兩根之和,進(jìn)而求出中點(diǎn)的橫坐標(biāo),代入直線求出中點(diǎn)的縱坐標(biāo),進(jìn)而求出![]() 的中垂線的方程.令
的中垂線的方程.令![]() 求出P的縱坐標(biāo),即m的表達(dá)式,分斜率大于0和小于0兩種情況用均值不等式求出
求出P的縱坐標(biāo),即m的表達(dá)式,分斜率大于0和小于0兩種情況用均值不等式求出![]() 的取值范圍.
的取值范圍.
解:(1)由題意知:![]() ,
,![]() ,
,![]() ,解得:
,解得:![]() ,
,![]() ,
,
所以橢圓的方程為:![]() ;
;
(2)
直線![]() 的斜率必存在,
的斜率必存在,
若![]() ,則
,則![]() 為
為![]() 軸所在的直線,此時(shí)
軸所在的直線,此時(shí)![]() .
.
若![]() , 設(shè)直線l的方程為:
, 設(shè)直線l的方程為:![]() ,設(shè)
,設(shè)![]() ,
,![]() ,
,
聯(lián)立直線與橢圓的方程整理得:![]() ,
,![]() ,
,
所以中點(diǎn)E的橫坐標(biāo)為![]() ,
,
代入直線可得E的縱坐標(biāo) ,
,
所以![]() 的垂直平分線方程為:
的垂直平分線方程為: ,與
,與![]() 聯(lián)立可得
聯(lián)立可得 ,所以
,所以 ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() ,
,![]() ,故
,故 .
.
所以![]() 的取值范圍為
的取值范圍為 .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知某企業(yè)生產(chǎn)某種產(chǎn)品的年固定成本為200萬(wàn)元,且每生產(chǎn)1噸該產(chǎn)品需另投入12萬(wàn)元,現(xiàn)假設(shè)該企業(yè)在一年內(nèi)共生產(chǎn)該產(chǎn)品![]() 噸并全部銷售完.每噸的銷售收入為
噸并全部銷售完.每噸的銷售收入為![]() 萬(wàn)元,且
萬(wàn)元,且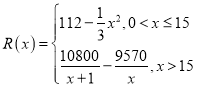 .
.
(1)求該企業(yè)年總利潤(rùn)![]() (萬(wàn)元)關(guān)于年產(chǎn)量
(萬(wàn)元)關(guān)于年產(chǎn)量![]() (噸)的函數(shù)關(guān)系式;
(噸)的函數(shù)關(guān)系式;
(2)當(dāng)年產(chǎn)量為多少噸時(shí),該企業(yè)在這一產(chǎn)品的生產(chǎn)中所獲年總利潤(rùn)最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱臺(tái)![]() 中,
中,![]() ,G,H分別為
,G,H分別為![]() ,
,![]() 上的點(diǎn),平面
上的點(diǎn),平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
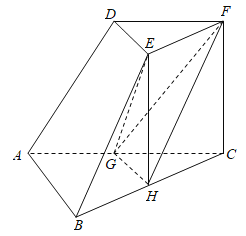
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系xOy中,點(diǎn)P到兩點(diǎn)(0,![]() ),(0,
),(0,![]() )的距離之和為4,設(shè)點(diǎn)P的軌跡為C,直線y=kx+1與A交于A,B兩點(diǎn).
)的距離之和為4,設(shè)點(diǎn)P的軌跡為C,直線y=kx+1與A交于A,B兩點(diǎn).
(1)寫出C的方程;
(2)若![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】“大眾創(chuàng)業(yè),萬(wàn)眾創(chuàng)新”是李克強(qiáng)總理在本屆政府工作報(bào)告中向全國(guó)人民發(fā)出的口號(hào),某生產(chǎn)企業(yè)積極響應(yīng)號(hào)召,大力研發(fā)新產(chǎn)品,為了對(duì)新研發(fā)的一批產(chǎn)品進(jìn)行合理定價(jià),將該產(chǎn)品按事先擬定的價(jià)格進(jìn)行試銷,得到一組銷售數(shù)據(jù)![]() ,如表所示:
,如表所示:
試銷單價(jià)x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
產(chǎn)品銷量y(件) | q | 84 | 83 | 80 | 75 | 68 |
已知![]()
(Ⅰ)求出q的值;
(Ⅱ)已知變量x,y具有線性相關(guān)關(guān)系,求產(chǎn)品銷量y(件)關(guān)于試銷單價(jià)x(元)的線性回歸方程![]() ;
;
(Ⅲ)用![]() 表示用(Ⅱ)中所求的線性回歸方程得到的與
表示用(Ⅱ)中所求的線性回歸方程得到的與![]() 對(duì)應(yīng)的產(chǎn)品銷量的估計(jì)值.當(dāng)銷售數(shù)據(jù)
對(duì)應(yīng)的產(chǎn)品銷量的估計(jì)值.當(dāng)銷售數(shù)據(jù)![]() 對(duì)應(yīng)的殘差的絕對(duì)值
對(duì)應(yīng)的殘差的絕對(duì)值![]() 時(shí),則將銷售數(shù)據(jù)
時(shí),則將銷售數(shù)據(jù)![]() 稱為一個(gè)“好數(shù)據(jù)”.現(xiàn)從6個(gè)銷售數(shù)據(jù)中任取3個(gè),求“好數(shù)據(jù)”個(gè)數(shù)
稱為一個(gè)“好數(shù)據(jù)”.現(xiàn)從6個(gè)銷售數(shù)據(jù)中任取3個(gè),求“好數(shù)據(jù)”個(gè)數(shù)![]() 的分布列和數(shù)學(xué)期望
的分布列和數(shù)學(xué)期望![]() .
.
(參考公式:線性回歸方程中![]() 最小二乘估計(jì)分別為
最小二乘估計(jì)分別為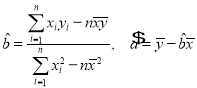 )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
,![]() 的最大值為
的最大值為![]() .
.
(1)求![]() 的值;
的值;
(2)試推斷方程![]() 是否有實(shí)數(shù)解?若有實(shí)數(shù)解,請(qǐng)求出它的解集.
是否有實(shí)數(shù)解?若有實(shí)數(shù)解,請(qǐng)求出它的解集.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】臨近開(kāi)學(xué)季,某大學(xué)城附近的一款“網(wǎng)紅”書(shū)包銷售火爆,其成本是每件15元.經(jīng)多數(shù)商家銷售經(jīng)驗(yàn),這款書(shū)包在未來(lái)1個(gè)月(按30天計(jì)算)的日銷售量![]() (個(gè))與時(shí)間
(個(gè))與時(shí)間![]() (天)的關(guān)系如下表所示:
(天)的關(guān)系如下表所示:
時(shí)間( | 1 | 4 | 7 | 11 | 28 | … |
日銷售量( | 196 | 184 | 172 | 156 | 88 | … |
未來(lái)1個(gè)月內(nèi),前15天每天的價(jià)格![]() (元/個(gè))與時(shí)間
(元/個(gè))與時(shí)間![]() (天)的函數(shù)關(guān)系式為
(天)的函數(shù)關(guān)系式為![]() (且
(且![]() 為整數(shù)),后15天每天的價(jià)格
為整數(shù)),后15天每天的價(jià)格![]() (元/個(gè))與時(shí)間
(元/個(gè))與時(shí)間![]() (天)的函數(shù)關(guān)系式為
(天)的函數(shù)關(guān)系式為![]() (且
(且![]() 為整數(shù)).
為整數(shù)).
(1)認(rèn)真分析表格中的數(shù)據(jù),用所學(xué)過(guò)的一次函數(shù)、反比例函數(shù)的知識(shí)確定一個(gè)滿足這些數(shù)據(jù)![]() (個(gè))與
(個(gè))與![]() (天)的關(guān)系式;
(天)的關(guān)系式;
(2)試預(yù)測(cè)未來(lái)1個(gè)月中哪一天的日銷售利潤(rùn)最大,最大利潤(rùn)是多少?
(3)在實(shí)際銷售的第1周(7天),商家決定每銷售1件商品就捐贈(zèng)![]() 元利潤(rùn)
元利潤(rùn)![]() 給該城區(qū)養(yǎng)老院.商家通過(guò)銷售記錄發(fā)現(xiàn),這周中,每天扣除捐贈(zèng)后的日銷售利潤(rùn)隨時(shí)間
給該城區(qū)養(yǎng)老院.商家通過(guò)銷售記錄發(fā)現(xiàn),這周中,每天扣除捐贈(zèng)后的日銷售利潤(rùn)隨時(shí)間![]() (天)的增大而增大,求
(天)的增大而增大,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2020年春節(jié)前后,一場(chǎng)突如其來(lái)的新冠肺炎疫情在全國(guó)蔓延.疫情就是命令,防控就是責(zé)任.在黨中央的堅(jiān)強(qiáng)領(lǐng)導(dǎo)和統(tǒng)一指揮下,全國(guó)人民眾志成城、團(tuán)結(jié)一心,掀起了一場(chǎng)堅(jiān)決打贏疫情防控阻擊戰(zhàn)的人民戰(zhàn)爭(zhēng).下圖表展示了2月14日至29日全國(guó)新冠肺炎疫情變化情況,根據(jù)該折線圖,下列結(jié)論正確的是( )
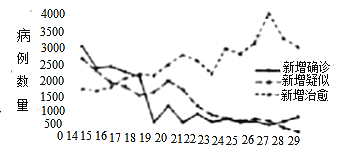
A.16天中每日新增確診病例數(shù)量呈下降趨勢(shì)且19日的降幅最大
B.16天中每日新增確診病例的中位數(shù)小于新增疑似病例的中位數(shù)
C.16天中新增確診、新增疑似、新增治愈病例的極差均大于2000
D.19日至29日每日新增治愈病例數(shù)量均大于新增確診與新增疑似病例之和
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義:首項(xiàng)為![]() 且公比為正數(shù)的等比數(shù)列為“
且公比為正數(shù)的等比數(shù)列為“![]() 數(shù)列”.
數(shù)列”.
(Ⅰ)已知等比數(shù)列![]() (
(![]() )滿足:
)滿足:![]() ,
,![]() ,判斷數(shù)列
,判斷數(shù)列![]() 是否為“
是否為“![]() 數(shù)列”;
數(shù)列”;
(Ⅱ)設(shè)![]() 為正整數(shù),若存在“
為正整數(shù),若存在“![]() 數(shù)列”
數(shù)列”![]() (
(![]() ),
),![]() 對(duì)任意不大于
對(duì)任意不大于![]() 的正整數(shù)
的正整數(shù)![]() ,都有
,都有![]() 成立,求
成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com